Атрактор Питера де Йонга представлен на странице https://cgraph.ru/node/151

Фрактал Питера де Йонга (Peter de Jong fractal) представляет собой итеративную систему в двух измерениях с четырьмя параметрами (a, b, c и d). Любой другой набор значений параметров порождает другой аттрактор. В дополнение к четырем параметрам также должен быть указан набор начальных условий. Определяющие уравнения следующие:
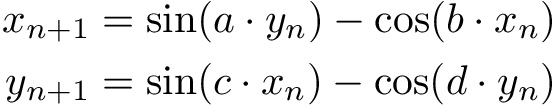
Каждая координата изменяется в зависимости от набора из двух уравнений, а также от положения предыдущей координаты.
Приведем примеры различных фракталов, в зависимости от параметров:
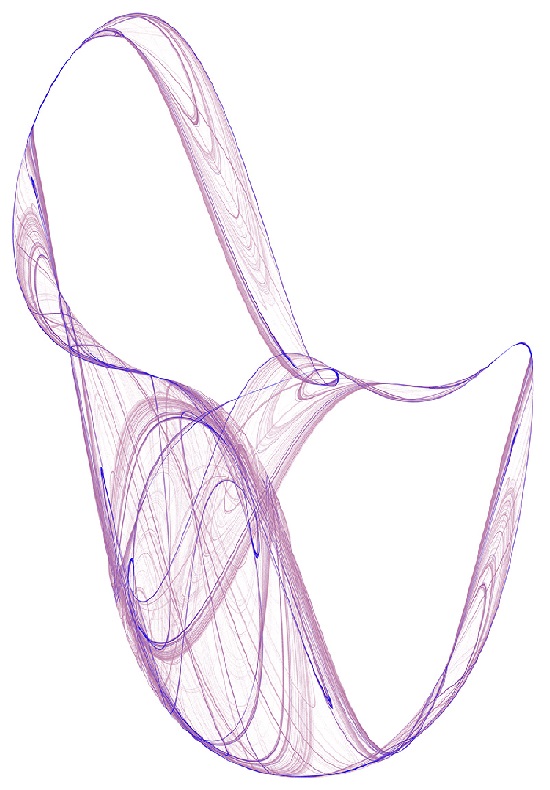
a = 1.641, b = 1.902, c = 0.316, d= 1.525

a = 1.4, b = -2.3, c = 2.4, d = -2.1

a = -2.24, b = 0.43, c = -0.65, d = -2.43
Характерной чертой различных аттракторов является независимость от начальных значений координат, при их изменении множество точек, сгенерированных согласно данным уравнениям, будет тоже. И лишь меняя значения констант получим различные отображения.




