Триангуляция Делоне множества точек - это такое разбиение множества точек на множество треугольников, что внутри окружности, описанной вокруг любого треугольника, не лежит ни одной точки из множества, кроме вершин самого треугольника.

Свойства:
- Триангуляция Делоне единственна
- Триангуляция Делоне максимизирует минимальный угол в треугольниках.
- Триангуляция Делоне максимизирует сумму радиусов вписанных окружностей.
Триангуляцию Делоне можно получить из любой другой триангуляции этого множества точек, устраняя нарушения определения. Для этого необходимо использовать операцию "флип", мы будем поворачивать ребро внутри пары смежных треугольников:
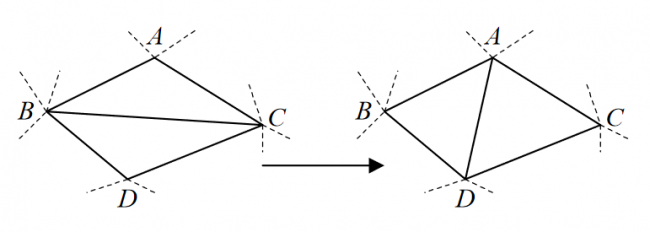
Рассмотрим алгоритмы построения триангуляции Делоне:
Итеративный алгоритм.
1. На первых трех точках строится треугольник.
2. Поочередно добавляются остальные точки.
2.1. Находится треугольник, в котором лежит эта точка. Если такого нет, то это треугольник, который находится ближе всего к ней.
2.2. Если точка совпадает с узлом триангуляции, то добавлять ее не нужно.
2.3. Если точка лежит на ребре триангуляции, то оно разбивается на два ребра. А треугольники, содержащие это ребро также разбиваются на два.
2.4. Если точка лежит строго внутри треугольника, то он разбивается на три новых.
3. Проводится проверка триангуляции на соответствие определению, при необходимости проводятся исправления операцией "флип".
Алгоритм "разделяй и властвуй".
Множество точек делится на две примерно равных части, для каждой из них строится триангуляция. Затем эти триангуляции склеиваются.
Алгоритм прямого построения (метод активных ребер).
1. Выбирается базовый отрезок AB, на основе которого будет построена триангуляция.
2. Ищется сосед Делон - узел, который вместе с концами базового отрезка будет являться треугольником в триангуляции Делоне. То есть выбирается такая точка Pi, что ∠APiB максимален.
3. Новые ребра помечаются базовыми отрезками. Процесс продолжается пока не будут добавлены все вершины.
Двупроходной алгоритм.
1. Строится триангуляция множества точек, но в процессе построения игнорируется проверка соответствия триангуляции определению триангуляции Делоне.
2. При помощи операции "флип" полученная триангуляция перестраивается, чтобы определение выполнялось.




