Среда программирования:
JavaScript
Статья по теме:
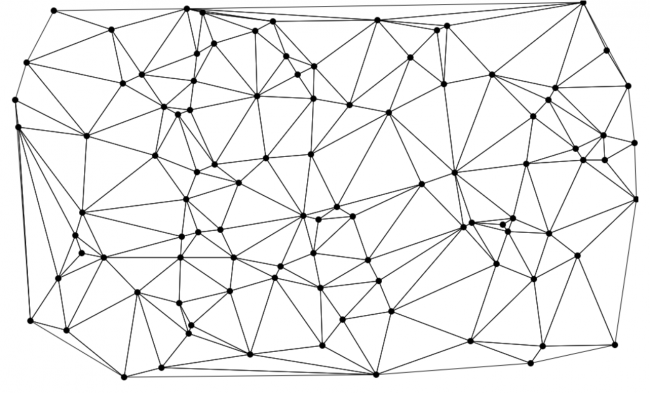
Задача: построить триангуляцию Делоне для множества точек.
Описание работы программы:
С помощью нормального распределения генерируется 100 точек, принадлежащих области канваса.
Затем находится треугольник, содержащий все точки этого множества.
После чего каждая точка последовательно добавляется в триангуляцию с необходимыми перестроениями триангуляции.
Код программы:
<!DOCTYPE html> <html lang="en"> <head> <meta charset="UTF-8"> </head> <body> <canvas width="1000" height="600"></canvas> <script> 'use strict'; let EPS = 1e-7; // эпсилон для работы с вещественными числами // подключение canvas let canvas = document.querySelector("canvas"); let ctx = canvas.getContext("2d"); // генерация точек множества при помощи нормального распределения const size = 100; let pts = []; for (let i = 0; i < size; i++) { let x = Math.random() * canvas.width, y = Math.random() * canvas.height; pts.push([Math.round(x), Math.round(y)]); } // функция, находящая треугольник, содержащий все точки множества function big_triangle(points) { let minx = 1000000, maxx = -1000000, miny = 1000000, maxy = -1000000; for (let i = 0; i < points.length; i++) { minx = Math.min(minx, points[i][0]); miny = Math.min(miny, points[i][1]); maxx = Math.max(maxx, points[i][0]); maxy = Math.max(maxy, points[i][1]); } let dx = maxx - minx, dy = maxy - miny; let dxy = Math.max(dx, dy); let midx = dx * 0.5 + minx, midy = dy * 0.5 + miny; return [ [midx - 10 * dxy, midy - 10 * dxy], [midx, midy + 10 * dxy], [midx + 10 * dxy, midy - 10 * dxy] ] } // вычисление центра и радиуса описанной окружности вокруг треугольника function circumcircle_of_triangle(points, v1, v2, v3) { //console.log(v1, v2, v3); let x1 = points[v1][0], y1 = points[v1][1]; let x2 = points[v2][0], y2 = points[v2][1]; let x3 = points[v3][0], y3 = points[v3][1]; let dy12 = Math.abs(y1 - y2), dy23 = Math.abs(y2 - y3); let xc, yc; if (dy12 < EPS) { let m2 = -((x3 - x2) / (y3 - y2)); let mx2 = (x2 + x3) / 2, my2 = (y2 + y3) / 2; xc = (x1 + x2) / 2, yc = m2 * (xc - mx2) + my2; } else if (dy23 < EPS) { let m1 = -((x2 - x1) / (y2 - y1)); let mx1 = (x1 + x2) / 2, my1 = (y1 + y2) / 2; xc = (x2 + x3) / 2, yc = m1 * (xc - mx1) + my1; } else { let m1 = -((x2 - x1) / (y2 - y1)), m2 = -((x3 - x2) / (y3 - y2)); let mx1 = (x1 + x2) / 2, my1 = (y1 + y2) / 2; let mx2 = (x2 + x3) / 2, my2 = (y2 + y3) / 2; xc = (m1 * mx1 - m2 * mx2 + my2 - my1) / (m1 - m2); if (dy12 > dy23) yc = m1 * (xc - mx1) + my1; else yc = m2 * (xc - mx2) + my2; } let dx = x2 - xc, dy = y2 - yc; return {'a': v1, 'b': v2, 'c': v3, 'x': xc, 'y': yc, 'r': dx*dx + dy*dy}; } // функция, удаляющая кратные ребра function delete_multiples_edges(edges) { for (let j = edges.length - 1; j >= 0;) { let b = edges[j]; j--; let a = edges[j]; j--; let n, m; for (let i = j; i >= 0;) { n = edges[i]; i--; m = edges[i]; i--; if (a === m && b === n) { edges.splice(j + 1, 2); edges.splice(i + 1, 2); break; } if (a === n && b === m) { edges.splice(j + 1, 2); edges.splice(i + 1, 2); break; } } } } // функция, находящая триангуляцию function triangulate(points) { let n = points.length; if (n < 3) return []; // треугольников нет points = points.slice(0); // копия массива // массив индексов, отсортированных по координате икс let ind = []; for (let i = 0; i < n; i++) ind.push(i); ind.sort(function(l, r) { return points[r][0] - points[l][0]; }) // находим треугольник, содержащий все точки, и вставлем его в конец массива с вершинами let big = big_triangle(points); points.push(big[0]); points.push(big[1]); points.push(big[2]); let cur_points = [circumcircle_of_triangle(points, n, n + 1, n + 2)]; let ans = []; let edges = []; // перебираем все точки for (let i = ind.length - 1; i >= 0; i--) { // перебираем все треугольники // если точка находится внутри треугольника, то нужно его удалить for (let j = cur_points.length - 1; j >= 0; j--) { // если точка справа от описанной окружности, то треугольник проверять больше не нужно // точки отсортированы и поэтому тоже будут справа let dx = points[ind[i]][0] - cur_points[j].x; if (dx > 0 && dx * dx > cur_points[j].r) { ans.push(cur_points[j]); cur_points.splice(j, 1); continue; } // если точка вне окружности, то треугольник изменять не нужно let dy = points[ind[i]][1] - cur_points[j].y; if (dx * dx + dy * dy - cur_points[j].r > EPS) { continue; } // удаляем треугольник и добавляем его стороны в список ребер edges.push( cur_points[j].a, cur_points[j].b, cur_points[j].b, cur_points[j].c, cur_points[j].c, cur_points[j].a ); cur_points.splice(j, 1); } // удаляем кратные ребра delete_multiples_edges(edges); // создаем новые треугольники последовательно по списку ребер for (let j = edges.length - 1; j >= 0;) { let b = edges[j]; j--; if (j < 0) break; let a = edges[j]; j--; cur_points.push(circumcircle_of_triangle(points, a, b, ind[i])); } edges = []; } // формируем массив с триангуляцией for (let i = cur_points.length - 1; i >= 0; i--) { ans.push(cur_points[i]); } let tr = [] for (let i = 0; i < ans.length; i++) { if (ans[i].a < n && ans[i].b < n && ans[i].c < n) { tr.push(ans[i].a, ans[i].b, ans[i].c); } } console.log(tr); return tr; } // отрисовка триангуляции console.log(pts); ctx.strokeStyle = "black"; let triangles = triangulate(pts); // отрисовка сгенерированных точек for (let i = 0; i < pts.length; i++) { ctx.beginPath(); ctx.arc(pts[i][0], pts[i][1], 5, 0, 2 * Math.PI); ctx.closePath(); ctx.fill(); } // отрисовка треугольников for (let i = 0; i < triangles.length;) { ctx.beginPath(); ctx.moveTo(pts[triangles[i]][0], pts[triangles[i]][1]); i++; ctx.lineTo(pts[triangles[i]][0], pts[triangles[i]][1]); i++; ctx.lineTo(pts[triangles[i]][0], pts[triangles[i]][1]); i++; ctx.closePath(); ctx.stroke(); } </script> </body> </html>
| Прикрепленный файл | Размер |
|---|---|
| novikov_delone_example_js.zip | 2.41 кб |




