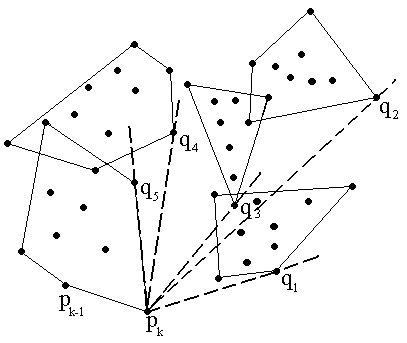
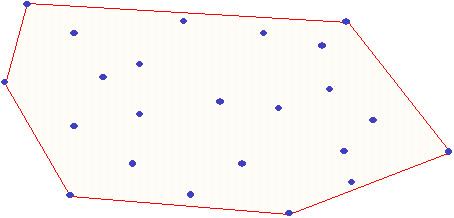
Пусть на плоскости задано некоторое количество точек. Оболочкой множества данных точек называется любая замкнутая линия, которая содержит в себе все эти точки.
Соответственно минимальная выпуклая оболочка - это такая оболочка, которая является выпуклым многоугольником наименьшего периметра.

В обработке изображений, распознавании образов и разработке игр часто возникает задача поиска выпуклой оболочки на плоскости. Для этого существуют следующие алгоритмы:
- Алгоритм обхода Джарвиса
- Алгоритм обхода Грэхема
- Алгоритм монотонных цепочек Эндрю
- Алгоритм типа «Разделяй и властвуй»
- Алгоритм «быстрого построения»
- Алгоритм Чана
Рассмотрим некоторые из них.
Алгоритм обхода Джарвиса
Пусть дан массив точек P.
- Необходимо найти точку, которая гарантировано будет входить в выпуклую оболочку; очевидно, что самая левая нижняя точка подходит под это условие.Находим точку с минимальной координатой x и y, и делаем ее текущей H[0].
- Перебираем все оставшиеся точки двойным циклом по i и j. В массив H записываем самую правую точку относительно вектора H[i]P[j]. Для этого находим векторное произведение, и если оно меньше 0, следовательно точка P[j] находится правее точки P[i] относительно H[i].
- Алгоритм завершается тогда, когда в H будет записана стартовая вершина и следовательно линия замкнется.
Псевдокод:
Jarvis(P)
1) H[1] = самая левая нижняя точка массива P;
2) i = 1;
3) do {
H[i+1] = любая точка из P (кроме уже попавших в выпуклую оболочку, но включая p[1]);
for (для каждой точки j из P, кроме уже попавших в выпуклую оболочку, но включая p[1])
if( векторное произведение(H[i], H[i+1], P[j]) < 0 ):
H[i+1] = P[j]
i = i + 1;
} while P[i] != P[1]
4) return p;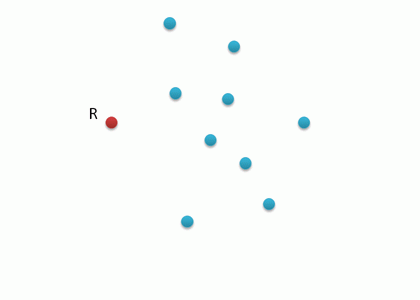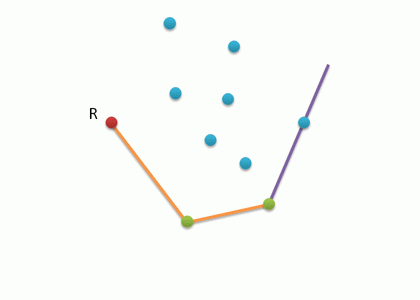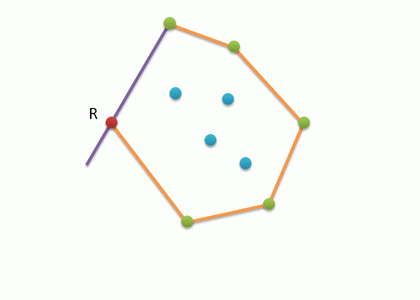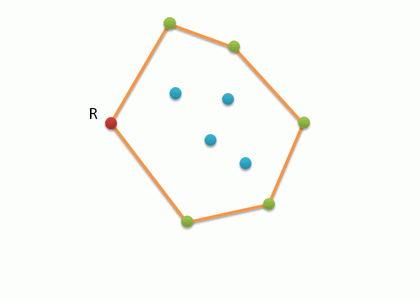
Сложность обхода Джарвиса - O(hn), где n - количество всех вершин и h - количество вершин попавших в выпуклую оболочку.
Алгоритм обхода Грэхема
Сложность данного алгоритма O(nlgn) - следовательно он будет работать быстрее обхода Джарвиса.
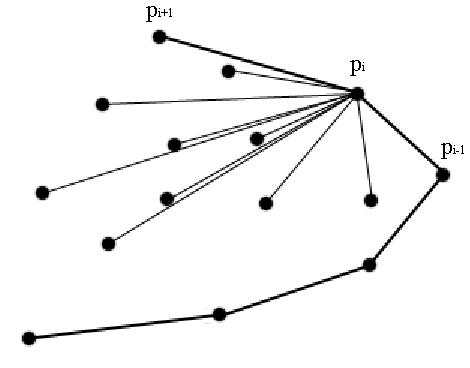
1. Как и в предыдущем алгоритме находим самую нижнюю левую точку и делаем ее начальной.
2. Сортируем все оставшиеся точки в порядке их “левизны” относительно начальной точки, с помощью векторного произведения.
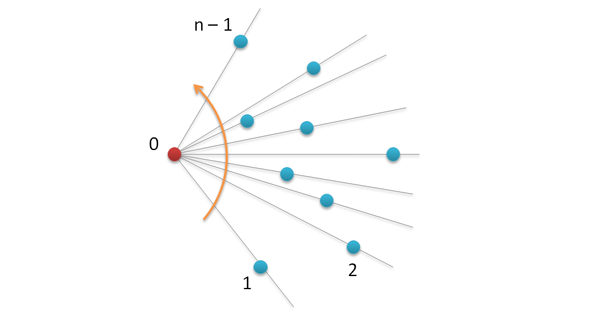
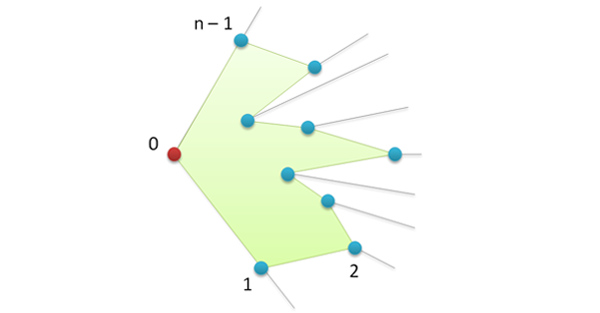
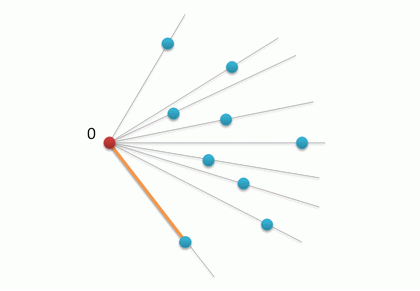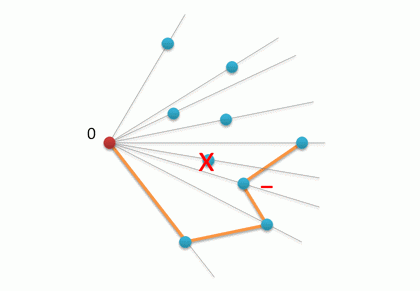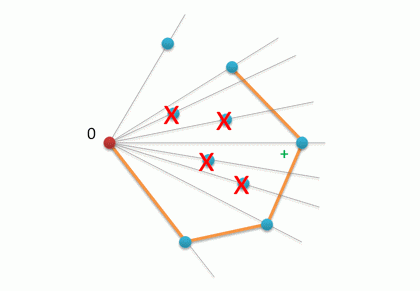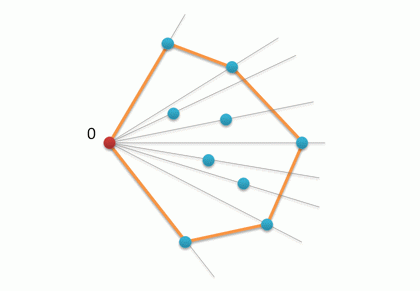
3. Как мы видим, получился многоугольник и для того, чтобы сделать его выпуклым необходимо убрать все те точки, в которых выполняется правый поворот (опять же, с помощью векторного произведения).
Код алгоритма на javascript:
function graham() { var minI = 0; //номер нижней левой точки var min = points[0].x; // ищем нижнюю левую точку for (var i = 1; i < points.length; i++) { if (points[i].x < min) { min = points[i].x; minI = i; } } // делаем нижнюю левую точку активной ch[0] = minI; ch[minI] = 0; // сортируем вершины в порядке "левизны" for (var i = 1; i < ch.length - 1; i++) { for (var j = i + 1; j < ch.length; j++) { var cl = classify({ 'x1': points[ ch[0] ].x, 'y1': points[ ch[0] ].y, 'x2': points[ ch[i] ].x, 'y2': points[ ch[i] ].y }, points[ ch[j] ].x, points[ ch[j] ].y) // функция classify считает векторное произведение. // если векторное произведение меньше 0, следовательно вершина j левее вершины i.Меняем их местами if (cl < 0) { temp = ch[i]; ch[i] = ch[j]; ch[j] = temp; } } } //записываем в стек вершины, которые точно входят в оболочку h = []; h[0] = ch[0]; h[1] = ch[1]; for (var i = 2; i < ch.length; i++) { while (classify({ 'x1': points[ h[h.length - 2] ].x, 'y1': points[ h[h.length - 2] ].y, 'x2': points[ h[h.length - 1] ].x, 'y2': points[ h[h.length - 1] ].y }, points[ ch[i] ].x, points[ ch[i] ].y) < 0) { h.pop(); // пока встречается правый поворот, убираем точку из оболочки } h.push(ch[i]); // добавляем новую точку в оболочку } }
Метод Эндрю.
В методе обхода Грэхема имеется один недостаток: при упорядочении точек используется сравнение углов. Чтобы исправить этот недостаток, Эндрю предложил следующую модификацию метода обхода Грэхема, в которой вместо сравнения углов применяется сравнение абсцисс точек.
Пусть задано конечное множество M точек плоскости, состоящее из m элементов. Сначала находятся его левая крайняя точка l и правая крайняя точка r этого множества. Для определенности среди точек с наименьшей абсциссой выбирается точка с наименьшей ординатой, а среди точек с наибольшей абсциссой — точка с наибольшей ординатой. Построим прямую, проходящую через точки l и r (см. рис. 1). Множество M разбивается на два подмножества, первое из которых состоит из точек, расположенных выше прямой, и называется верхним подмножеством, а второе состоит из остальных точек и называется нижним подмножеством.
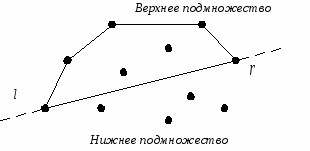
Рис.1. Разбиение, определенное крайними точками
Строится выпуклая оболочка верхнего подмножества вместе с точками l и r. Затем строится выпуклая оболочка нижнего подмножества и точек l и r. В результате получаем две ломанные, которые вместе составляют выпуклый многоугольник, ограничивающий искомую выпуклую оболочку.
Выпуклая оболочка верхнего подмножества и точек l и r строится в два этапа:
Верхние точки вместе с точками l и r сортируются по возрастанию абсцисс. Среди точек с одинаковой абсциссой оставляется лишь верхняя.
Производится просмотр троек pipi+1pi+2 верхних точек. Если вектор pipi+1 расположен слева от pipi+2, то увеличивается i, в противном случае точка pi+1 удаляется из списка (или массива) верхних точек.
Есть еще более быстрый способ поиска - алгоритм Чана. Его идея заключается в том, чтобы разбить множество заданных точек на группы, по m точек в каждой. Для каждой из таких групп строится выпуклая оболочка обходом Грэхема. Затем находится самая нижняя левая точка, и методом Джарвиса строится общая оболочка для всех групп, при этом следующая точка находится быстрее, так как в каждой группе они отсортированы в нужном порядке после обхода Грэхема. Следовательно для нахождения следующей точки оболочки нужно проверить только одну точку из каждой группы.