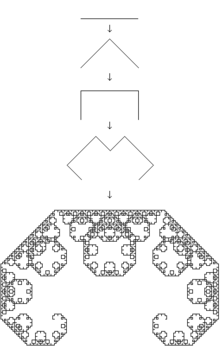
Кривая Леви — фрактал. Впервые изучено итальянецем Эрнесто Чезаро в 1906 году. Однако его самоподобие и фрактальные свойства исследовал французский математик П. Леви в 1930-х годах.
За сходство с буквой «С», написанной витиеватым шрифтом, ее еще называют С-кривой Леви.
- Кривая Леви нигде не дифференцируема и не спрямляема.
- На любом интервале кривой Леви есть точки самопересечения.
- Хаусдорфова размерность кривой Леви приблизительно равна 1,9340. (Хотя кривая Леви состоит из двух равных частей, каждая из которых подобна всей кривой с коэффициентом подобия 1/\sqrt2, из-за наличия самопересечений её размерность меньше чем 2=\ln 2/\ln \sqrt 2.)
- Кривая Леви — крона дерева Пифагора.