
Данный фрактал был придуман мной и мне захотелось его изобразить. Построение производится по аналогии с Т-фракталом.
Фрактал представляет собой множество соприкасающихся кругов, в целом фрактал частично напоминает клевер, отсюда и название.
ПостроениеИзначально имеем круг некоторого радиуса(назовем его родителем). Затем слева, сверху и справа от родителя касаются его круги-потомки с радиусом, вдвое меньше а далее для каждого последующего потомка процедура повторяется по 3-м точкам касания(4-я точка касания с родителем).
Данную процедуру демонстрирует рисунок ниже.
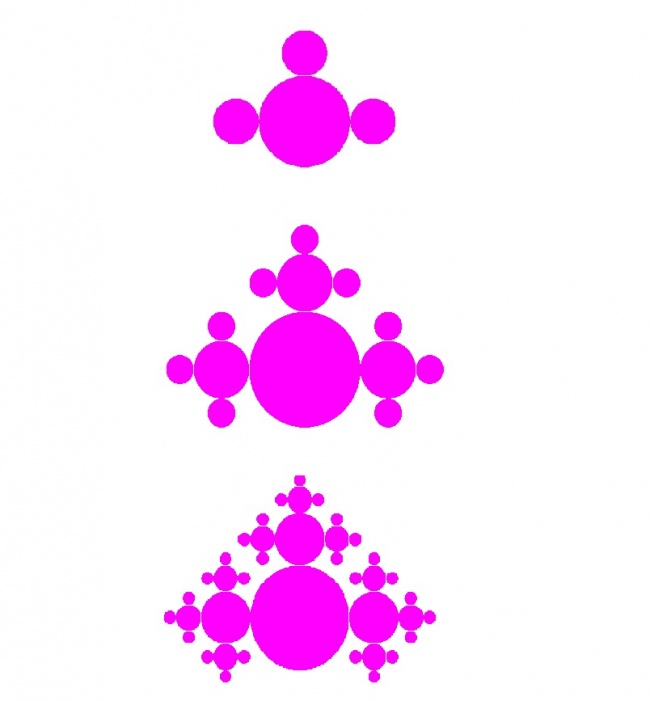
- Квазиклевер самоподобен
- Ни один из кругов не имеет более одной точки пересечения с другим кругом
- Потомки разных родителей никогда не касаются друг друга
- Площадь фрактала равна 4πR2, где R - радиус родителя(находится с помощью суммы бесконечного ряда)




