Суть алгоритма поиска в ширину в том, что мы обходим связный граф таким образом, что сначала мы рассматриваем родителя, потом по очереди рассматриваем его предков, потом рассматриваем предков его предков и т.д.
Порядок обхода вершин графа.
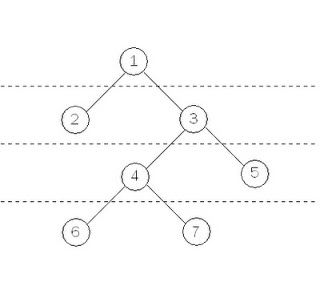
Можно объяснить алгоритм двумя способами:
Первой вершине (родителю всех остальных вершин) приписываем метку 1. Рассматриваем все смежные с ней вершины и приписываем им метку 2. Дальше рассматриваем окружение вершин с меткой 2 и присваиваем метку 3 всем вершинам, кроме самой главной (родителя всех вершин).
Второй способ объяснения (по моему более понятнее, ну по крайней мере писать его легче) подразумевает под собой имитирование «горения» графа. Т.е. мы поджигаем самую первую вершину, дальше огонь перекидывается на смежные с ней вершины, с них на смежные с ними и т.д.
Рассмотрим алгоритм поиска в ширину для заполнения ограниченных областей.
Поиск в ширину является одним из методов обхода графа.
Описание алгоритма:
1) В очередь помещается стартовая вершина и помечается как посещенная.
2) Пока очередь не опустеет, берем первое значение и делаем все возможные переходы из этой вершины, добавляя их в очередь и помечая использованными.
3) Удаляем вершину, которую рассматривали.
Для этих же целей можно было бы использовать и алгоритм поиску в глубину, и хотя он реализовывается в несколько строк, он очень требователен к памяти, поэтому мы и остановились на алгоритме поиска в ширину.
Работа программы:
До вызова BFS:
После вызова BFS: