Площадь многоугольника

Ориентированная площадь треугольника – это обычная площадь, снабженная знаком. Знак ориентированной площади треугольника АВС такой же, как у ориентированного угла между векторами AB и AC. То есть ее знак зависит от порядка перечисления вершин.

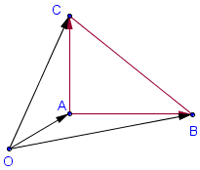
Рисунок №1

На рис. 1 треугольник АВС – прямоугольный. Его ориентированная площадь равна S=|OB||OC|/2(она больше нуля, так как пара OB,OC ориентирована положительно). Эту же величину можно вычислить другим способом.

Пусть О – произвольная точка плоскости. На рисунке площадь треугольника ABC получится, если из площади треугольника OBC вычесть площади OAB и OCA. Таким образом, нужно просто сложить ориентированные площади треугольников OAB, OBC и OCA. Это правило работает при любом выборе точки О.

Точно так же для вычисления площади любого многоугольника A₁A₂...A_n нужно сложить ориентированные площади треугольников OA₁A₂,OA₂A₃,...,OA_nA₁

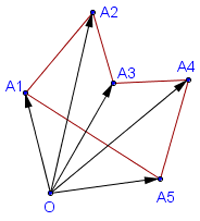
Рисунок №2

В сумме получится площадь многоугольника, взятая со знаком плюс, если при обходе ломаной A₁A₂...A_n многоугольника находится слева (обход границы против часовой стрелки), и со знаком минус, если он находится справа (обход по часовой стрелке).

Итак, вычисление площади многоугольника свелось к нахождению площади треугольника. Теперь необходимо выразить ее в координатах.

Векторное произведение двух векторов на плоскости есть площадь параллелограмма, построенного на этих векторах.

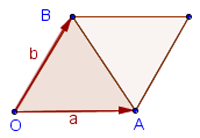
Рисунок №3

Векторное произведение, выраженное через координаты векторов:

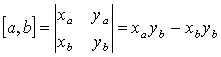
Площадь треугольника будет равна половине этой площади:

S=1/2(x_ay_b-y_ax_b)

В качестве точки О удобно взять начало координат, тогда координаты векторов, на основании которых вычисляются ориентированные площади, совпадут с координатами точек.

Пусть (х₁, y₁), (x₂, у₂), ..., (х_n,у_n) —координаты вершин заданного многоугольника в порядке обхода по или против часовой стрелки. Тогда его ориентированная площадь S будет равна:

S=1/2(x₁y₂-y₁x₂+x₂y₃-y₂x₃+...+x_ny₁-y_nx₁)

Это и есть рабочая формула.

Если координаты вершин были заданы в порядке обхода против часовой стрелки, то число S, вычисленное по этой формуле, получится положительным. В противном случае оно будет отрицательным, и для получения обычной геометрической площади необхо­димо взять его абсолютное значение.