Среда программирования:
Lazarus
Статья по теме:
Построение лямбда-фрактала.
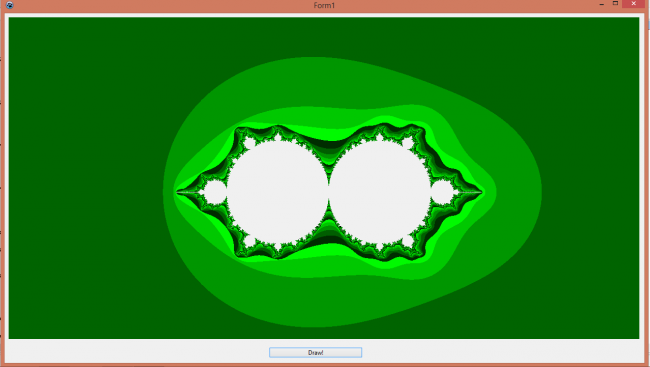
Рассмотрим множество Мандельброта при f(z)=(lambda)*z*(1-z), при z0=0.5.
На форме находится кнопка " Draw! " . При нажатии на нее получаем изображение лямбда-фрактала.
Код программы:
unit Unit1; {$mode objfpc}{$H+} interface uses Classes, SysUtils, FileUtil, Forms, Controls, Graphics, Dialogs, StdCtrls, ExtCtrls; type { TForm1 } TForm1 = class(TForm) Button1: TButton; PaintBox1: TPaintBox; procedure Button1Click(Sender: TObject); private { private declarations } public { public declarations } end; var Form1: TForm1; implementation {$R *.lfm} { TForm1 } procedure TForm1.Button1Click(Sender: TObject); type TComplex = record //типизированные константы X : Real; Y : Real; end; const //после какого количества шагов, функция должна прекрать работу iterations = 50; max = 4; var z, c : TComplex; //комплексные переменные x, y, n : Integer; p, q : Real; //переменные для описания числа лямбда xc, yc : Integer; //координаты центра PaintBox1 colour: TColor; //цвет фрактала begin with PaintBox1.Canvas do Begin Clear; //очищаем PaintBox1 xc := Width div 2; //находим координаты центра PaintBox1 yc := Height div 2; // проходим каждый пиксель диапазона на экране for y := -yc to yc do for x := -xc to xc do begin n := 0; //выбираем значения константы С, от значения которой зависит форма лямбда-фрактала c.x := x * 0.01 + 1; c.y := y * 0.01; //начальное (нулевое) значение действительной и мнимой частей комплексного числа z z.x := 0.5; z.y := 0; //вычисляем реальную и мнимую части числа z и числа лямбда while (sqr(z.x) + sqr(z.y) < max) and (n < iterations) do begin //Lambda p := z.x - sqr(z.x) + sqr(z.y); q := z.y - 2 * z.x * z.y; z.x := c.x * p - c.y * q; z.y := c.x * q + c.y * p; n:=n+1; end; if (n < iterations) then begin //выбираем цвет по числу итераций colour := (n * 50) mod 255; Pixels[xc+x,yc+y]:=RGBToColor(0,colour,0); end; end; end; end; end.
| Прикрепленный файл | Размер |
|---|---|
| Stus_lambda_mandelbrot.rar | 1.24 Мб |




