Среда программирования:
Lazarus
Статья по теме:
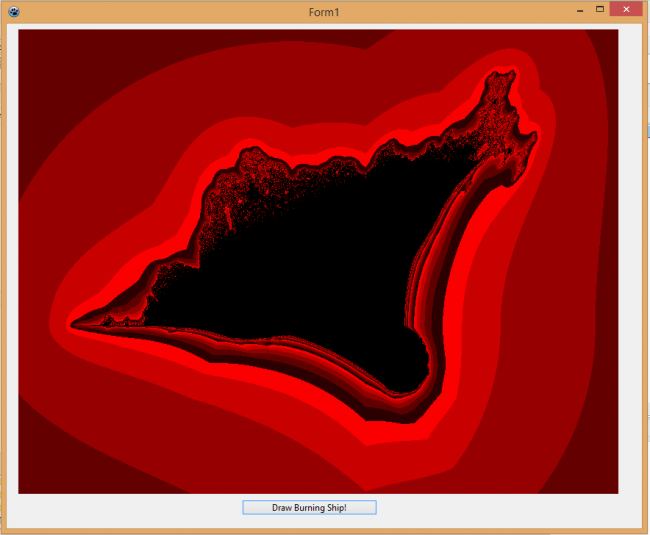
Задача: создание фрактала "Горящий Корабль".
Фрактал является генерацией итеративной функции в комплексной плоскости С:
Zn+1=(|Re(Zn)|-i|Im(Zn)|)2 + C, Z0=0
Код программы:
unit Unit1; {$mode objfpc}{$H+} interface uses Classes, SysUtils, FileUtil, Forms, Controls, Graphics, Dialogs, StdCtrls, ExtCtrls; type { TForm1 } TForm1 = class(TForm) Button1: TButton; PaintBox1: TPaintBox; procedure Button1Click(Sender: TObject); private { private declarations } public { public declarations } end; var Form1: TForm1; implementation {$R *.lfm} { TForm1 } procedure TForm1.Button1Click(Sender: TObject); type TComplex = record //типизированные константы X : Real; Y : Real; end; const //после какого количества шагов, функция должна прекрать работу iterations = 30; max = 16; var z, t, c : TComplex; //комплексные переменные x, y, n : Integer; xc, yc : Integer; //координаты центра PaintBox1 r,g,b : Integer; //цвета для задания в палитре RGB begin //закрасим PaintBox1 черным цветом //чтобы заливка корабля была черной, а не белой PaintBox1.Canvas.Brush.Color := clBlack; Paintbox1.Canvas.Rectangle(0,0,PaintBox1.Width, PaintBox1.Height); with PaintBox1.Canvas do Begin xc := Width div 2; //находим координаты центра PaintBox1 yc := Height div 2; // проходим каждый пиксель диапазона на экране for y := -yc to yc do for x := -xc to xc do begin n := 0; //установим начальное значение константы С //которая определяет форму фрактала c.x := x * 0.005 - 0.2; c.y := y * 0.005 - 0.3; //начальное значение действительной и мнимой частей числа Z z.x := 0; z.y := 0; //вычисляем реальную и мнимую части числа z while (sqr(z.x) + sqr(z.y) < max) and (n < iterations) do begin //запоминаем предыдущее значение t := z; //вычисление в текущем значении n < iterations z.x := sqr(t.x) - sqr(t.y) + c.x; z.y := 2 * abs(t.x * t.y) + c.y; n:=n+1; end; if n < iterations then begin //выбираем цвет по числу итераций //можно выбрать одно из значений переменной color //для изoбражения фрактала в разной цветовой палитре r := (50 * n) mod 256; g := (80 * n) mod 256; b := (120 * n) mod 256; //Pixels[xc+x,yc+y]:=RGBToColor(r,g,b); Pixels[xc+x,yc+y]:=RGBToColor(r,0,0); end; end; end; end; end.
| Прикрепленный файл | Размер |
|---|---|
| Stus_burning_ship.rar | 1.24 Мб |




