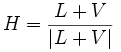Подробнее https://cgraph.ru/node/435
Локальные и глобальные модели освещенияОпределение. Луч, который приходит непосредственно от источника света, называется первичным. Луч, который претерпел одно или несколько переотражений, называется вторичным. Физические модели, которые не учитывают перенос света между поверхностями (не используют вторичное освещение), называются локальными. В противном случае модели называются глобальными или моделями глобального освещения.
Физически обоснованные и эмпирические модели освещенияФизически обоснованные модели материалов. Физически обоснованные модели стараются аппроксимировать свойства некоторого реального материала. Такие модели учитывают особенности поверхности материала, например слои материала (моделирование кожи или тонких пленок) или же поведение частиц материала (моделирование снега, песка, различных жидкостей).
Эмпирические модели материалов. Эмпирические модели устроены несколько иначе, чем физически обоснованные. Как правило, данные модели подразумевают некий набор параметров, не имеющих физической интерпретации, но позволяющих с помощью подгона получить нужный вид конечной модели. Иногда такие модели дают более качественный результат за счет большего контроля за выразительностью, чем за точностью.
Примеры эмпирических моделей: модель Ламберта, модель Фонга.
Самая простая модель освещения может быть построена, как сумма таких световых составляющих.

I = Ia+Id+Is ,
где
Ia - фоновая составляющая (ambient);
Id - рассеянная составляющая (diffuse);
Is - зеркальная составляющая (specular).

Фоновое освещение это постоянная в каждой точке величина надбавки к освещению. Вычисляется фоновая составляющая освещения как:
Ia = ka • ia ,
где
Ia – фоновая составляющая освещенности в точке,
ka – свойство материала воспринимать фоновое освещение,
ia – мощность фонового освещения.
Из формулы выше видно, что фоновая составляющая освещенности не зависит от пространственных координат освещаемой точки и источника. Часто просто задается некое глобальное фоновое освещение всей сцены.
Модель ЛамбертаМодель Ламберта моделирует идеальное диффузное освещение. Считается, что свет при попадании на поверхность рассеивается равномерно во все стороны. При расчете такого освещения учитывается только ориентация поверхности (нормаль N) и направление на источник света (вектор L). Рассеянная составляющая рассчитывается по закону косинусов (закон Ламберта):
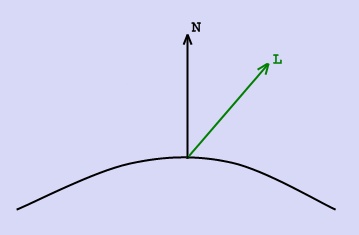
Для удобства все векторы, описанные ниже, берутся единичными. В этом случае косинус угла между ними совпадает со скалярным произведением.
![]()
где
Id– рассеянная составляющая освещенности в точке,
kd– свойство материала воспринимать рассеянное освещение,
id– мощность рассеянного освещения,
L – направление из точки на источник,
N - вектор нормали в точке.
Модель Ламберта является одной из самых простых моделей освещения. Данная модель очень часто используется в комбинации других моделей, практически в любой другой модели освещения можно выделить диффузную составляющую. Более-менее равномерная часть освещения (без присутствия какого-либо всплеска) как правило будет представляться моделью Ламберта с определенными характеристиками. Данная модель может быть очень удобна для анализа свойств других моделей (за счет того, что ее легко выделить из любой модели и анализировать оставшиеся составляющие).
Модель ФонгаМодель Фонга – классическая модель освещения. Модель представляет собой комбинацию диффузной составляющей (модели Ламберта) и зеркальной составляющей и работает таким образом, что кроме равномерного освещения на материале может еще появляться блик. Местонахождение блика на объекте, освещенном по модели Фонга, определяется из закона равенства углов падения и отражения. Если наблюдатель находится вблизи углов отражения, яркость соответствующей точки повышается.
Падающий и отраженный лучи лежат в одной плоскости с нормалью к отражающей поверхности в точке падения, и эта нормаль делит угол между лучами на две равные части. Т.о. отраженная составляющая освещенности в точке зависит от того, насколько близки направления на наблюдателя и отраженного луча. Это можно выразить следующей формулой:
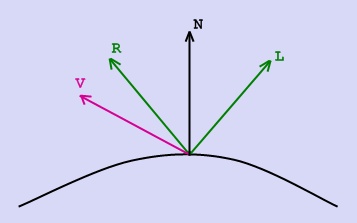
Прим. В общем случае вектора V, L и N не лежат в одной плоскости.
![]()
где
Is – зеркальная составляющая освещенности в точке,
ks – коэффициент зеркального отражения,
is – мощность зеркального освещения,
R – направление отраженного луча,
V - направление на наблюдателя,
α - коэффициент блеска, свойство материала.
Модель Блинна-Фонга – это унификация модели Фонга, исключающая расчет отраженного луча, что упрощает вычисления. Принципиальной разницы между двумя этими моделями нет.
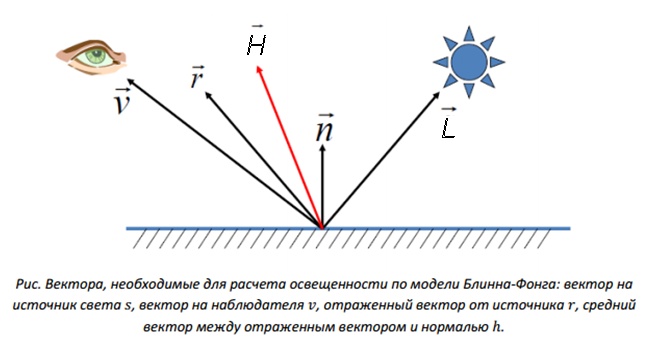
![]()
где вектор H является «медианой» угла между векторами V и L.
Вектор H вычисляется по формуле: