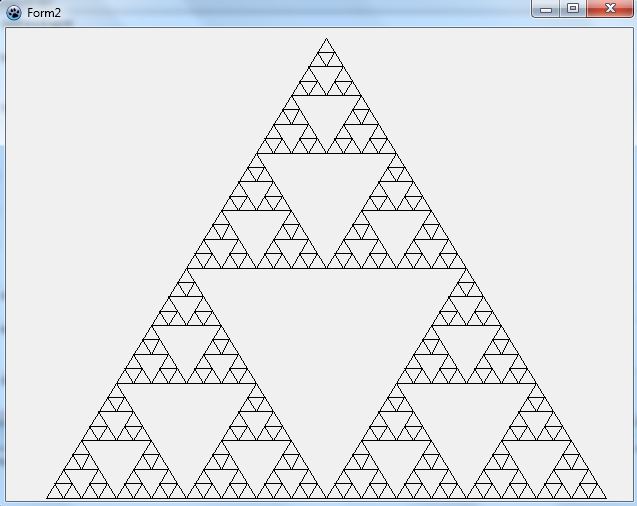
В 1915 году польский математик Вацлав Серпинский придумал занимательный объект, известный как решето Серпинского. Этот треугольник один из самых ранних известных примеров фракталов. Существует несколько способов построения этого фрактала. Один из них представляет следующий процесс. Берётся сплошной равносторонний треугольник, на первом шаге из центра удаляется перевёрнутый треугольник. На втором шаге удаляется три перевёрнутых треугольника из трёх оставшихся треугольников. Продолжая этот процесс, на n-ом шаге удаляем 3^(n-1)перевёрнутых треугольников из центров 3^(n-1)оставшихся треугольников. Конца этому процессу не будет, и в треугольнике не останется живого места, но и на части он не распадётся - получится объект состоящий из одних только дырок. Это и есть треугольник Серпинского. Треугольник Серпинского также называют салфеткой Серпинского.
unit Unit1; {$mode objfpc}{$H+} interface uses Classes, SysUtils, FileUtil, Forms, Controls, Graphics, Dialogs, StdCtrls, ExtCtrls; type { TForm1 } TForm1 = class(TForm) Button1: TButton; PaintBox1: TPaintBox; procedure Button1Click(Sender: TObject); private { private declarations } procedure tr(x1, y1, x2, y2, x3, y3: integer); procedure draw(x1, y1, x2, y2, x3, y3: Real; n: real); public { public declarations } end; const iter = 6; var Form1: TForm1; implementation {$R *.lfm} procedure TForm1.tr(x1, y1, x2, y2, x3, y3: integer); begin paintbox1.canvas.moveto(x1,y1); paintbox1.canvas.lineto(x2,y2); paintbox1.canvas.moveto((x2),round(y2)); paintbox1.canvas.lineto(round(x3),round(y3)); paintbox1.canvas.moveto(round(x3),round(y3)); paintbox1.canvas.lineto(round(x1),round(y1)); end; procedure TForm1.draw(x1, y1, x2, y2, x3, y3: Real; n: real); var x1n, y1n, x2n, y2n, x3n, y3n : Real; begin if n > 0 then begin x1n := (x1 + x2) / 2; y1n := (y1 + y2) / 2; x2n := (x2 + x3) / 2; y2n := (y2 + y3) / 2; x3n := (x3 + x1) / 2; y3n := (y3 + y1) / 2; tr(trunc(x1n), trunc(y1n), trunc(x2n), trunc(y2n), trunc(x3n), trunc(y3n)); draw(x1, y1, x1n, y1n, x3n, y3n, n - 1); draw(x2, y2, x1n, y1n, x2n, y2n, n - 1); draw(x3, y3, x2n, y2n, x3n, y3n, n - 1); end; end; procedure TForm1.Button1Click(Sender: TObject); begin tr(320,10,600,470,40,470); draw(320,10,600,470,40,470,iter);{} end; end.
| Прикрепленный файл | Размер |
|---|---|
| Исходные коды и запускаемый файл | 762.98 кб |




