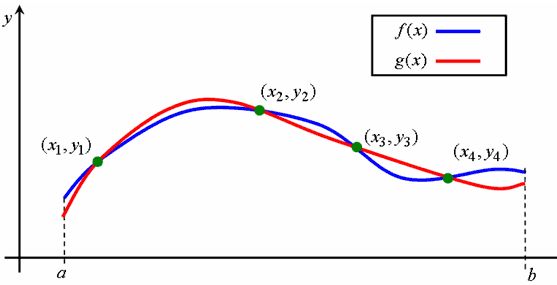
Многочлен Ньютона интерполяционный – как и другие интерполяционные формулы, служит для построения многочлена n-й степени, который совпадает в (n+1) точке co значениями неизвестной искомой функции у = f(x).
Пусть в точках х0, х1, …, хn+1 значения функции у = f(x) равны соответственно у0 = f(x0), y1 = f(x1), …, yn+1 = f(xn+1).
Построим интерполяционный многочлен Ньютона с помощью метода неопределенных коэффициентов. Для этого запишем искомый многочлен в виде
Pn(x) = b0 + b1(x – x0) + b2(x – x0)(x – x1) + b3(x – x0)(x – x1)(x – x2) + … + bn(x – x0)…(x – xn).(1)
Последовательно подставляя в формулу (1) вместо х данные значения х0, х1, ..., хn+1, получим для нахождения неопределенных коэффициентов b0, b1, ..., bn «треугольную» систему уравнений
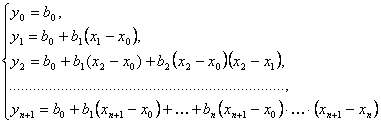
При подстановке в равенство (1) вместо х числа х0 в правой части равенства обратились в нуль все слагаемые, кроме первого: там везде был множитель (х – х0), обратившийся в нуль; при подстановке х = х1 обратились в нуль все слагаемые, кроме первого и второго – они содержат множитель (х – х1) и т.д.
Полученную систему удобно решать: из первого её уравнения находим свободный член искомого многочлена b0; подставив его во второе уравнение, находим коэффициент b1 при первой степени х в искомом многочлене:
![]()
и т.д.
Для интерполяционного многочлена Ньютона можно выписать явные выражения коэффициентов через данные задачи, а также и оценки точности замены неизвестной функции f(x) этим многочленом.




