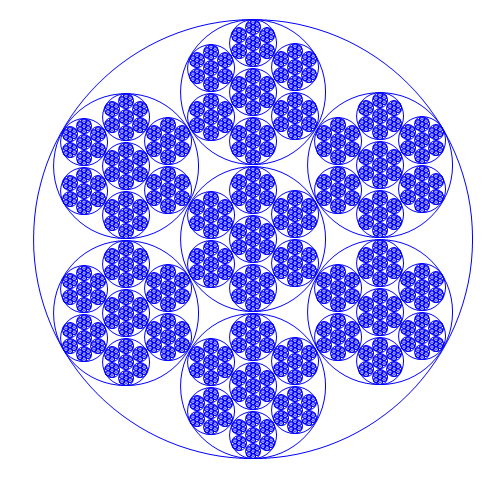
Круговой фрактал — класс геометрических (конструктивных) фракталов, построенных многократным вписыванием в окружность других окружностей меньшего радиуса.
Применение
Конструктивные круговые фракталы могут найти применение в качестве моделей различных природных структур в химии, биологии, технологии материалов и др. Фракталы такого типа были предложены в работе в качестве моделей кластеров магнитопотоковых трубок в верхних слоях солнечной конвективной зоны. Рассматривались и более сложные конструкции такого рода, например, круговые фракталы с перекрывающимися элементами, моделирующие скрученные магнитопотоковые трубки. Возможно также построение мультифрактальных конструкций подобного типа для моделирования более сложных структур. В отличие от ковров Серпинского, такие фракталы строятся не из прямоугольных или треугольных, а из круговых элементов.
Первые три из потенциально бесконечной последовательности таких круговых фракталов приведены на рисунках ниже.
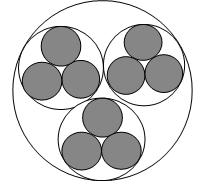
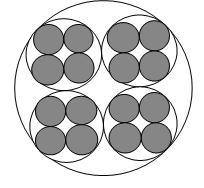
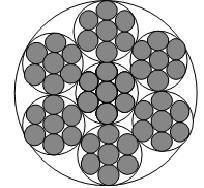
Для расчета хаусдорфовых размерностей (d) этих объектов можно воспользоваться известной формулой для конструктивных фракталов: d=log(n)/log(1/a) . В случае первого рисунка значение n=3. Параметр а — отношение характерных длин соседних масштабов. В данном случае, это r_{i+1}/r_i; где r_i — радиус большей окружности, r_{i+1} — радиус окружности соседнего меньшего масштаба. Из простых геометрических соображений находим: а=0,4641. Подставляя эти значения в формулу, получаем d≈1,43. Для варианта на втором рисунке, соответственно, n=4, а=0,4142… , d≈1,57… Для варианта, изображенного на третьем рисунке, имеем: n=7, a=1/3 и, размерность d≈1,77… Увеличивая число вписываемых окружностей, получаем бесконечную последовательность фрактальных объектов, с хаусдорфовыми размерностями d → 2.
Алгоритм
В окружность радиуса R вписывают семь окружностей радиуса R/3 таким образом, чтобы они все касались, но не пересекали друг друга. В каждую из этих семи окружностей вписываются по семь окружностей R/9 и т. д. Смотрите примеры.




