Математический маятник

23. Май 2016 - 21:36 | Мельничук Антон

Колебания математического маятника с большой амплитудой представляют значительный
математический интерес. Данная механическая система (в отличии от системы, совершающей малые колебания, которые аппроксимируются гармоническими) нелинейна, т.к. в дифференциальном уравнении колебаний φ''=-ω²sinφ, угловое ускорение пропорционально синусу углового смещения; более того функция смещения от времени не выражается в элементарных функциях и называется синус Якоби.

На данной анимации видно, что график функции, полученный посредством физического моделирования не является графиком функции sinx.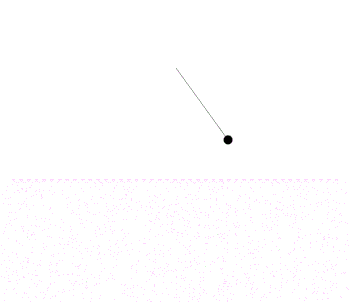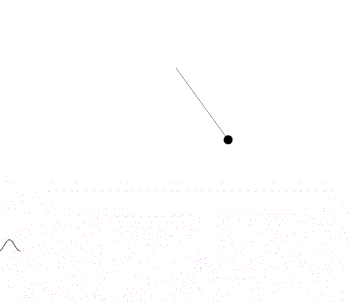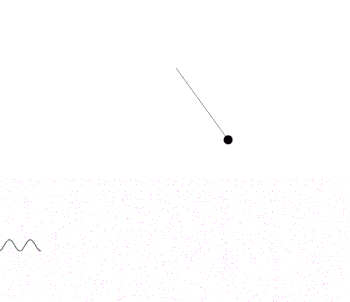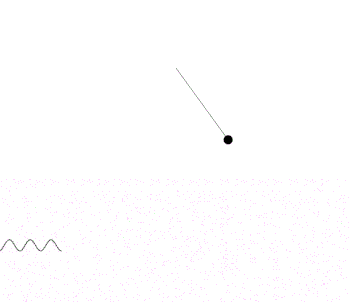
Однако, если уменьшить амплитуду колебаний, график в значительной степени приближается графиком sinx. Поэтому математический маятник, совершающий малые колебания, можно считать гармоническим осциллятором (ускорение пропорционально и направлено противоположно смещению) и описывать упрощенным законом φ''=-ω²φ. Тем не менее, т.к. больший интерес представляют именно нелинейные колебания интегрировать численно будем общий закон φ''=-ω²sinφ.
Интегрируем предельно просто - по методу Эйлера.

function update(){
	bob.a = -(g/L)*Math.sin(bob.phi)
	bob.v +=  bob.a*dt
	bob.phi += bob.v*dt
        t += dt
}

Здесь bob - объект, свойства которого

bob = {
	phi: initPhi,
	v: 0,
	a: 0
}

соответственно угол отклонения, угловая скорость и ускорение. ω² = -(g/L), где g - ускорение свободного падения (придется выражать в пикселях на секнду в квадрате), L - длина стержня. Отсюда, кстати, следует, что период колебаний не зависит от амплитуды, которая в свою очередь не зависит от массы груза. Для тех, кто подзабыл школьную физику - вот вывод уравнения колебаний, которое мы, собственно, и интегрируем. Т.е. численное решение дифференциального уравнения по Эйлеру - это интуитивно понятное пошаговое суммирование ускорения с шагом dt и получение таким образом скорости, а затем скорости и получение приблизительного отклонения phi для каждого фрейма. Думаю, что процесс получения графика фукции углового отклонения от времени объяснять не стоит. Вот весь код:

<html>
<body>
<style>
	* { padding: 0; margin: 0; }
	canvas {display: block; margin: 0 auto; }
</style>
<canvas id="canvas"></canvas>
<canvas id="canvas2" style="background: #eee"></canvas>
</body>
<script>
var canvas = document.getElementById("canvas")
var canvas2 = document.getElementById("canvas2")
var ctx = canvas.getContext("2d")
var ctx2 = canvas2.getContext("2d")
var h = canvas.height = 500
var w = canvas.width = 600
var h2 = canvas2.height = 300
var w2 = canvas2.width = 800
ctx.translate(w/2,h/2)
ctx2.translate(0,h2/2)
ctx2.beginPath()
ctx2.moveTo(0,0)
 
var initPhi = Math.PI*0.2
var L = 200
var dt = 1/60
var g = 1500
var t = 0
 
bob = {
	phi: initPhi,
	v: 0,
	a: 0
}
function drawPendulum(){
	ctx.beginPath()
	ctx.arc(Math.sin(bob.phi)*L,Math.cos(bob.phi)*L,10,0,2*Math.PI)
	ctx.fill()
	ctx.moveTo(0,0)
	ctx.lineTo(Math.sin(bob.phi)*L,Math.cos(bob.phi)*L)
	ctx.stroke()
}
function update(){
	bob.a = -(g/L)*Math.sin(bob.phi)
	bob.v +=  bob.a*dt
	bob.phi += bob.v*dt
    t += dt
}
function drawGraph(){
 ctx2.lineTo(t*20,(bob.phi%Math.PI)*20 )
 ctx2.stroke()
}
function draw(){
	ctx.clearRect(-w/2,-h/2,w,h)
	drawPendulum()
	update()
    drawGraph()
	requestAnimationFrame(draw)
}
draw()
</script>
</html>

Хотелось бы привести еще один пример. Пример эмпирического моделирования, целью которого является не точность траектории, а "реалистичность" визуального эффекта. Такой прием широко распространен, к примеру, в компьютерных играх. Если вы внимательно прочитаете код предыдущего примера, то заметите, что маятнику не от чего останавливаться, т.е. трение стержня о подвес не реализовано. И хоть реализовать его не составит труда, можно провести моделирование следующим образом, убив сразу 2-х зайцев: интегрировать движение грузика, учитывая только силу тяжести (т.е. он каждый фрейм пытается оторваться и нарушить движение по окружности), а затем возвращать его, разрешая ограничение, наложенное на длину веревки. Только теперь придется суммировать векторы. Из-за неточности вычислений "бесплатно" получим еще и эффект затухания колебаний. Прикрепляю мой не очень удачный пример кода на Python с некоторыми вынужденными костылями. А вот гиф-анимация:

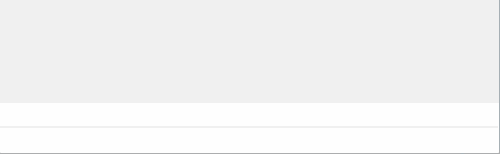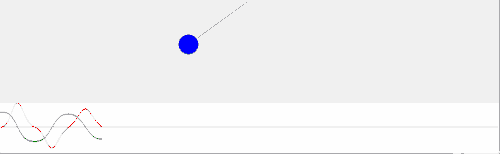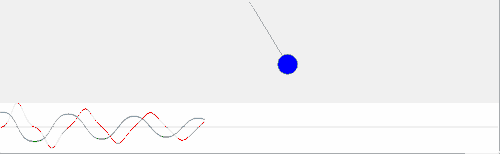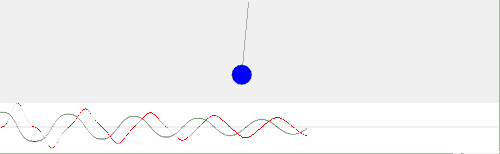
Прикрепленный файл	Размер
pendulum.rar	1.5 кб

Войдите на сайт для отправки комментариев

Физическое моделирование

	Построения на плоскости (2D)
	Графика в пространстве (3D)
	Вычислительная геометрия
	Физическое моделирование
	Фрактальная графика

Уроки, алгоритмы, программы, примеры

Материалы по разделам

Новые комментарии

Счетчики и рейтинг

Математический маятник

Комментарии