Данный алгоритм позволяет строить эллипсы на сновании координат центра фигуры и длин большей и меньшей полуосей.
Алгоритм является модификацией алгоритма для генерации окружностей.
Эллипс описывается каноническим уравнением X2/a2+Y2/b2=1 и для любого эллипса можно найти такую декартову систему координат, что это уравнение будет его описывать. При этом центр эллипса лежит в начале координат, а оси совпадают с координатными осями. При a=b данный алгоритм строит окружность, так как окружность действительно является частным случаем эллипса.
Как и в оригинальном алгоритме Брезенхема, выбор ближайшей точки основан на анализе знаков управляющих переменных, для вычисления которых используется исключительно целочисленная арифметика, что значительно повышает скорость выполнения алгоритма на любой ЭВМ.
Рассмотрим непосредственно алгоритм :
Для построения растровой развертки эллипса с осями, параллельными осям координат, и радиусами a, b воспользуемся каноническим уравнением X2/a2+Y2/b2=1 , которое перепишем в виде f(x, y) ≡ b2x2 + a2y2 – a2b2 = 0.
В отличие от окружности, для которой было достаточно построить одну восьмую ее часть, а затем воспользоваться свойствами симметрии, эллипс имеет только две оси симметрии, поэтому придется строить одну четверть всей фигуры. За основу возьмем дугу, лежащую между точками (0, b) и (a, 0) в первом квадранте координатной плоскости.
В каждой точке (x, y) эллипса существует вектор нормали, задаваемый градиентом функции f. Дугу разобьём на две части: первая – с углом между нормалью и горизонтальной осью больше 45○ (тангенс больше 1) и вторая – с углом, меньшим 45○ (Рис.1).
Движение вдоль дуги будем осуществлять по часовой стрелке, начиная с точки (0, b).
Направление нормали соответствует вектору grad(x, y) = (∂f/∂x, ∂f/∂y) = (2b2x, 2a2y).
Отсюда находим тангенс угла наклона вектора нормали: t = a2y/b2x. Приравнивая его единице, получаем что координаты точки деления дуги на вышеуказанные части удовлетворяют равенству b2x = a2y. Поэтому критерием того, что мы переходим ко второй области будет соотношение a2(y-1/2) ≤ b2(x+1) (координаты дополнительной точки (x+1, y-1/2) (Рис.2)), или , переходя к целочисленным операциям, a2(2y-1) ≤ 2b2(x+1).
Вдоль всей дуги координата Y является монотонно убывающей, но в первой части дуги она убывает медленнее, чем растёт X, а во второй быстрее. Поэтому в первой части дуги будем сначала увеличивать значение X, а во второй сначала уменьшать значение Y.
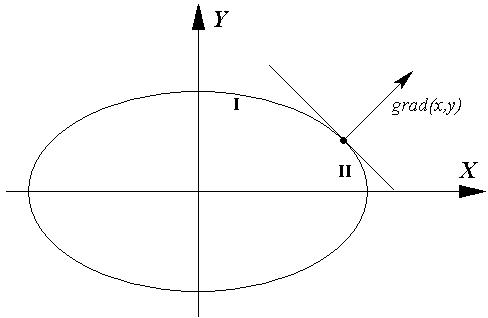
Рис.1 Деление дуги на 2 части
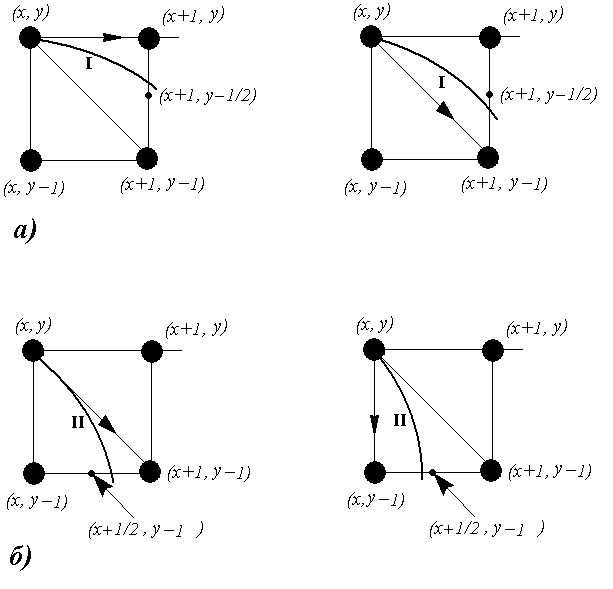
Рис.2 Способы поставить следующий пиксел
При перемещении вдоль первого участка дуги мы каждый раз переходим либо по горизонтали, либо по диагонали, критерий перехода напоминает тот, который используется при построении окружности. Находясь в точке (x, y), будем увеличивать значение X на единицу, а затем вычислять значение ∆ = f(x+1, y-1/2). Если это значение меньше нуля, то дополнительная точка (x+1, y-1/2) находится внутри эллипса, следовательно, ближайшая точка растра есть (x+1, y), в противном случае это точка (x+1, y-1) (Рис2. а)).
На втором участке дуги возможен переход либо по вертикали, либо по диагонали, поэтому здесь сначала уменьшаем значение Y, затем вычисляем ∆ = f(x+1/2, y-1), и направление перехода выбирается аналогично предыдущему случаю (Рис2. б)).
Остаётся, чтобы перейти к целочисленной арифметике, оптимизировать вычисление параметра ∆, умножив его на 4 и представив в виде функции координат точки, тогда для первой части дуги получим:
∆ (x, y)= 4b2(x+1)2+a2(2y-1)2-4a2b2
∆ (x+1, y)= ∆ (x, y)+4b2(2x+3)
∆ (x+1, y-1)= ∆ (x, y)+4b2(2x+3)-8a2(y-1)
Для второй половины дуги получим:
∆ (x, y)= b2(2x+1)2+4a2(y+1)2-4a2b2
∆ (x, y-1)= ∆ (x, y)+4a2(2y+3)
∆ (x+1, y-1)= ∆ (x, y)+4a2(2y+3)-8b2(x+1)
Все оставшиеся дуги эллипса строятся параллельно: после получения очередной точки (x, y), можно инициализировать ещё три точки с координатами (-x, y), (x, -y), (-x, -y).
Достоинства алгоритма: высокая скорость работы, минимальное потребление памяти; значительная схожесть построенного эллипса с эллипс,нарисованным на непрерывной поверхности; использование исключительно целочисленной арифметики.
Недостатки алгоритма: необходима достаточная разрядность переменных при достаточно больших значениях a и b.




