Если абстрактно представить любой алгоритм заливки фигур (не специализированный для какой-то конкретной фигуры, а универсальный) то в нем обязательно обнаружится шаг с проверкой удовлетворяет ли выбранная точка некоторым условиям заливки. Чаще всего эти условия простые. Например, является ли цвет выбранной точки таким же, как и цвет точки, с которой началась заливка. Или еще проще — является ли выбранная точка отличной от цвета заливки. В этой статье предлагается сделать заливку более функциональной и «гибкой», изменив тривиальные условия заливки точки на более сложные. Мы не предлагаем более компактный или быстрый метод заливки, напротив, продемонстрированный ниже пример будет более ресурсозатратным по сравнению с обычными, однако будет предлагать более расширенный функционал, что хорошо подойдет, например, для редакторов изображений.
В качестве примера «нетривиальной проверки заливки» рассмотрим заливку с «жесткостью». Жесткость заливки — это параметр, который указывает на то, насколько значительные отклонения цвета в выбранной точке от цвета в начальной точке можно проигнорировать. Идея очень проста — поочередно считаем абсолютную разницу соответственных компонентов выбранного и начального цвета, выбираем из них наибольшую. Если наибольшая разность меньше параметра «жесткости», то закрашиваем точку.
Функция проверки жесткости на языке Java:
boolean ColorCompatibleByHardness(int pickedColor, int tagetColor, int fillColor, float maxHardness) {
// pickedColor – выбранный цвет
// tagetColor – начальный цвет
// fillColor – цвет заливки
// maxHardness – жесткость заливки от 0 до 1
//проверяем, не пытаемся ли мы закрасить точку с цветом заливки
if(pickedColor == fillColor) {
return false;
}
//получаем компоненты выбранного цвета и начального цвета в виде массивов
float[] ac = new Color(pickedColor).getRGBComponents(new float[4]);
float[] bc = new Color(tagetColor).getRGBComponents(new float[4]);
float maxDiff = 0; //значение разности
//перебираем первые 3 компонента цветов – R, G и B, компонент прозрачности A нас не интересует
for(int i = 0; i < 3; i++) {
//если их абсолютная разница больше текущего значения разности, перезаписываем его
maxDiff = Math.max(Math.abs(ac[i] - bc[i]), maxDiff);
}
//возвращаем истину, если значение разности меньше либо равно максимально допустимому (параметру жесткости заливки)
return maxDiff <= maxHardness;
}Очевидно, что если параметр жесткости равен 0, то эта заливка не будет ничем отличаться от тривиальной. При значении 1 заливка будет игнорировать все барьеры и закрасит всю область целиком.
Примеры заливки изображений с использованием обычной заливки и заливки с жесткостью:
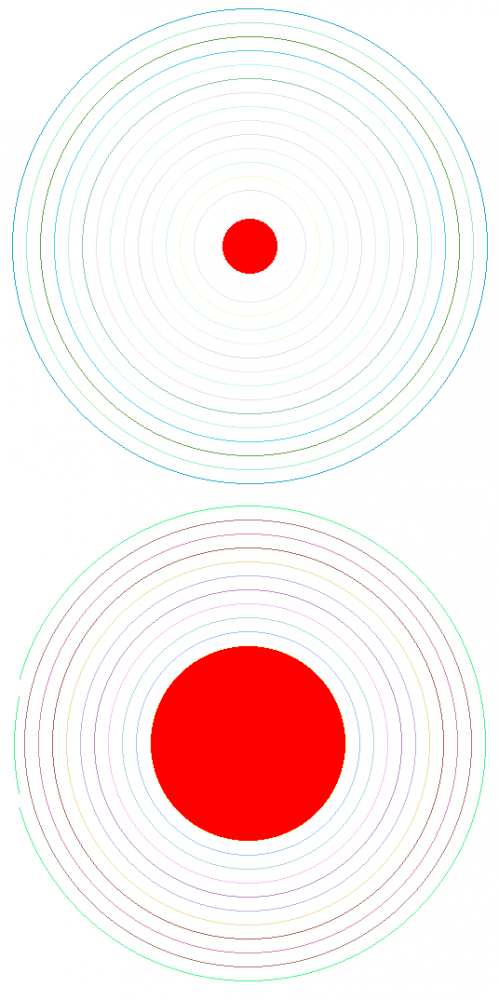
Рис. 1 Специально сконструированный полигон для тестирования заливки из окружностей от более тусклых цветов (приближенных к белому) до более насыщенных (с наибольшим приближением компонентов к максимальным значениям).

Рис. 2 Пример закраски дерева. На третьем изображении явно видно, что заливка с жесткостью почти полностью закрасила всю листву одним цветом, заливкой же без параметров (второе изображение) разноцветную листву закрасить невозможно.




