Среда программирования:
JavaScript
Статья по теме:
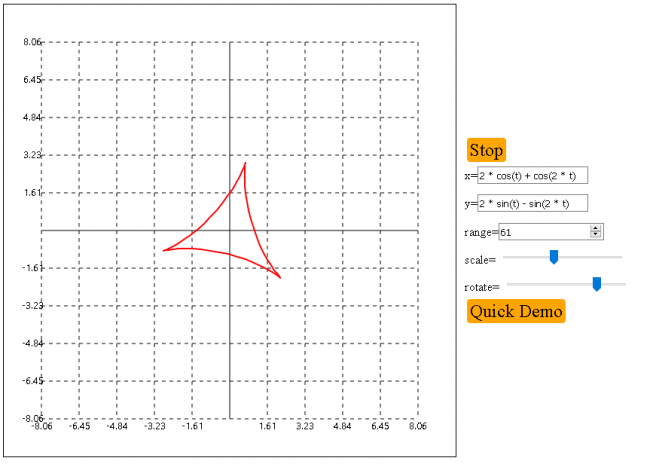
Программа реализует операции преобразования фигуры на плоскости, описанные в статье: параллельный перенос, поворот, масштабирование.
1. Файл grapher.html содержит HTML скелет программы: подключение необходимых библиотек, создание canvas'а для рисования и элементов управления графиком.
<!DOCTYPE html5> <html> <head> <meta charset="utf-8"> <link rel="stylesheet" href="grapher.css"> <script type="text/javascript" src="lib/jquery.min.js"></script> <script type="text/javascript" src="lib/jcanvas.min.js"></script> <script type="text/javascript" src="lib/math.min.js"></script> <script type="text/javascript" src="grapher.js"></script> <script type="text/javascript">$(() => init())</script> </head> <body> <table> <td> <canvas id="graph" width="600" height="600"></canvas> </td> <td> <a id="starter" class="btn" onClick="start();">Start</a> <div class="control">x=<input id="fx" type="text"></input></div> <div class="control">y=<input id="fy" type="text"></input></div> <div class="control">range=<input id="range" type="number"></input></div> <div class="control">scale=<input id="scale" type="range" min="10" max="60"></input></div> <div class="control">rotate=<input id="angel" type="range" min="0" max="360"></input></div> <a id="quick_show" class="btn" onClick="demo();">Quick Demo</a> </td> </table> </body> </html>
2. Файл grapher.js содержит всю логику программы
Код программы:
//элемент канваса, значение полей элементов упарвления var c, fx, fy, range, scale, angel; //html элементы упарвления var e_fx, e_fy, e_range, e_scale, e_angel; //центр канваса, в который переносится график var center = 300; //короткие названия функций var round = Math.round; var sin = Math.sin; var cos = Math.cos; var pi = Math.PI; //переменные для запуска/остановки процесса отрисовки графика var btnText = [ "Start", "Stop" ] var running = 0; var inter; //получаем необходимые html элементы function init() { c = $('#graph'); e_fx = $('#fx'); e_fy = $('#fy'); e_range = $('#range'); e_scale = $('#scale'); e_angel = $('#angel'); } //запуск/остановка процесса отрисовки графика function start() { //если отрисовка уже происходит, то останавливаем её if (running) { running = 0; window.clearInterval(inter); } else { running = 1; inter = setInterval(() => { //получаем значения html элементов fx = e_fx.val(); fy = e_fy.val(); range = Number(e_range.val()); scale = Number(e_scale.val()); angel = Number(e_angel.val()) / 180; c.clearCanvas(); drawNet(); var curve = { strokeStyle: 'red', strokeWidth: 2 }; /* получаем матрицу преобразования для точек 1ый арг == масштаб 2ой арг == вектор сдвига 3ой арг == точка, вокрун которой просходит вращение, а также угол вращения */ var adjuster = get_adjuster( scale, {x:center / scale, y:center / scale}, {x:center / scale, y:center / scale, a:angel}); for (var i = 0; i <= range; i++) { t = i / 10; p = [] p.push(eval(fx)); p.push(eval(fy)); //высчитываем точки графика, затем преобразовываем их p = adjust(p, adjuster); curve['x' + (i + 1)] = round(p[0]); curve['y' + (i + 1)] = round(p[1]); } //рисуем график на канвасе c.drawLine(curve); }, 50); } $('#starter').text(btnText[running]); } //функция отрисовки плоскости(сетки) масштаба function drawNet() { for (var i = 50; i <= 550; i += 50) { if (i === center) continue; c.drawLine({ strokeStyle: '#000', strokeWidth: 1, strokeDash: [5], strokeDashOffset: 0, x1: 50, y1: i, x2: 550, y2: i }).drawLine({ strokeStyle: '#000', strokeWidth: 1, strokeDash: [5], strokeDashOffset: 0, x1: i, y1: 50, x2: i, y2: 550 }).drawText({ fillStyle: '#000', fontSize: 13, fontFamily: 'Segoe UI', text: ((center - i) / scale).toFixed(2), x: 38, y: i }).drawText({ fillStyle: '#000', fontSize: 13, fontFamily: 'Segoe UI', text: ((i - center) / scale).toFixed(2), x: i, y: 560 }); } c.drawLine({ strokeStyle: '#000', strokeWidth: 1, x1: center, y1: 50, x2: center, y2: 550 }).drawLine({ strokeStyle: '#000', strokeWidth: 1, x1: 50, y1: center, x2: 550, y2: center }); } //функция высчитывания матрицы преобразования function get_adjuster(mult, moveTo = { x:0, y:0 }, rotate = {x:0, y:0, a:0}) { var mv = math.matrix([ [1, 0, 0], [0, 1, 0], [moveTo.x, moveTo.y, 1]]); var sc = math.matrix([ [mult, 0, 0], [0, mult, 0], [0, 0, 1]]); var mvrt = math.matrix([ [1, 0, 0], [0, 1, 0], [-rotate.x, -rotate.y, 1]]); var mvrtbk = math.matrix([ [1, 0, 0], [0, 1, 0], [rotate.x, rotate.y, 1]]); var rt = math.matrix([ [cos(rotate.a * pi), sin(rotate.a * pi), 0], [-sin(rotate.a * pi), cos(rotate.a * pi), 0], [0, 0, 1]]); var mm = math.multiply; return mm(mm(mm(mm(mv, mvrt), rt), mvrtbk), sc); } //фунцкия применения матрицы преобразования к точке function adjust(point, adj_matrix) { point.push(1); return math.multiply(point, adj_matrix)._data.splice(0, 2); } //пример для наглядности работы function demo() { e_fx.val("2 * cos(t) + cos(2 * t)"); e_fy.val("2 * sin(t) - sin(2 * t)"); e_range.val("62"); e_scale.val("50"); e_angel.val("0"); start(); }
| Прикрепленный файл | Размер |
|---|---|
| grapher.zip | 168.69 кб |




