Растровый алгоритм Брезенхема построения линии

Алгоритм Брезенхема смотрите на странице https://cgraph.ru/node/181

Алгоритм Брезенхема (англ. Bresenham's line algorithm) — это алгоритм, определяющий, какие точки двумерного растра нужно закрасить, чтобы получить близкое приближение прямой линии между двумя заданными точками. Это один из старейших алгоритмов в машинной графике — он был разработан Джеком Е. Брезенхемом (Jack E. Bresenham) в компании IBM в 1962 году. Алгоритм широко используется, в частности, для рисования линий на экране компьютера.

В алгоритме используется управляющая переменная d_i, которая на каждом шаге пропорциональна разности между s и t (см. рис.1). На рисунке 1 приведен i-ый шаг, когда пиксель P_i-1 уже найден как ближайший к реальному изображаемому отрезку, и теперь требуется определить, какой из пикселей должен быть установлен следующим: T_i или S_i.

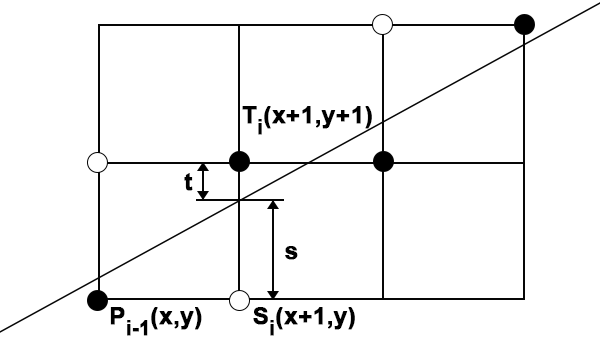
Рис.1

Если s < t, то S_i ближе к отрезку и необходимо выбрать его; в противном случае ближе находится T_i. Другими словами, если s -t < 0, то выбирается S_i; иначе выбирается T_i.

Отрезок в примере (на рис.1) проводится из точки (x₁, y₁) в точку (x₂, y₂). Пусть первая точка находится ближе к началу координат, тогда вычтем из соответствующих координат x₁ и y₁ тем самым перенеся первую точку в начало координат, тогда конечная окажется в (Δx, Δy), где Δx = x₂ - x₁, Δy = y₂ - y₁. Уравнение прямой теперь имеет вид y = x(Δy / Δx). В рассматриваемом примере предполагается, что Δx >= Δy и Δy >= 0.

Из рисунка 1 следует, что

s = (Δy / Δx)(x + 1) - y,

t = y + 1 - (Δy / Δx)(x + 1)

поэтому

s - t = 2( Δy / Δx)(x + 1) - 2y - 1.

Домножим обе части равенства на Δx:

Δx(s - t) = 2(Δy•x - y•Δx) + 2Δy - Δx.

Так как Δx > 0, то величину Δx(s-t) можно использовать в качестве критерия для выбора пикселя. Обозначим эту величину d_i:

d_i = 2(Δy•x_i-1 - y_i-1•Δx) + 2Δy - Δx.

Так как d_i надо считать на каждом шаге, рассчитаем величину Δ_i — приращения d_i:

Δ_i = d_i - d_i-1 = 2Δy(x_i - x_i-1) - 2Δx(y_i - y_i-1).

Известно, что x_i – x_i-1 = 1.

Если d_i >= 0, то выбираем T_i, т.е. y_i — y_i-1 = 1 (перемещаем точку по y), а Δ_i тогда равно

Δ_i = 2(Δy - Δx).

Если d_i < 0, то выбираем S_i, т.е. y_i — y_i-1 = 0 (у не меняется), тогда Δ_i = 2Δy.

Таким образом, мы получили итеративную формулу для вычисления критерия d_i.

Начальное значение d₁ = 2Δy - Δx.

Важно учитывать, что такой алгоритм требует определения ещё одного параметра — значения, определяющего изменение y_i. В примере мы предполагали Δy >= 0, а потому при перемещении точки изменяли значение на +1. Если значение Δy < 0, то изменение происходит на -1.

Аналогично рассматривается случай, когда Δx < Δy. Алгоритм Брезенхэма в своей реализации требует учёт всех возможных ситуаций взаимного расположения точек.

Procedure line (x1, y1, x2, y2: Integer);
var dx, dy, d, d1, d2, x, y, stp: Integer;
begin
  dx := x2 - x1;
  dy := y2 - y1;
  if ((abs(dx) > abs(dy)) and (x2 < x1))
    or ((abs(dx) <= abs(dy)) and (y2 < y1)) then begin
      x := x1;
      x1 := x2;
      x2 := x;
      y := y1;
      y1 := y2;
      y2 := y;
  end;
  dx := x2 - x1;
  dy := y2 - y1;
  stp := 1;
  putpixel(x1, y1, clblack);
  if (abs(dx) > abs(dy)) then begin
    if (dy < 0) then begin
      stp := -1;
      dy := -dy;
    end;
    d := (dy * 2) - dx;
    d1 := dy * 2;
    d2 := (dy - dx) * 2;
    y := y1;
    for x := x1 + 1 to x2 do begin
      if (d > 0) then begin
        y := y + stp;
        d := d + d2;
      end else
        d := d + d1;
      putpixel(x, y, clblack);
    end;
  end else begin
    if (dx < 0) then begin
      stp := -1;
      dx := -dx;
    end;
    d := (dx * 2) - dy;
    d1 := dx * 2;
    d2 := (dx - dy) * 2;
    x := x1;
    for y := y1 + 1 to y2 do begin
      if (d > 0) then begin
        x := x + stp;
        d := d + d2;
      end else
        d:=d+d1;
      putpixel(x, y, clblack);
    end;
  end;
end;