Для работы используется модифицированный алгоритм Брезенхейма для построения прямых. Обрабатываемый многоугольник обязательно должен быть невырожденным. Заливка произойдёт в любом случае, однако если у многоугольника есть самопересечения, то алгоритм может отработать некорректно. Алгоритм не чувствителен к порядку обхода, в котором заданы вершины многоугольника.
Суть модификации в том, чтобы отмечать все граничные точки в массиве, после чего отсекающий алгоритм избавится от лишних точек и оставит только такие, по которым алгоритм закраски сможет однозначно сказать, должен ли быть закрашен текущий пиксель. Алгоритм не повреждает фоновое изображение и работает за O(N*M) времени, где N и M — максимальное расстояние между двумя точками по вертикали и горизонтали соответственно.
Проход алгоритма осуществляется по каждой вертикальной линии многоугольника, возможно построение аналогичного алгоритма для горизонтальных линий.
Приведена специальная модификация, благодаря которой алгоритм может закрашивать круги, используя при построении модифицированный алгоритм Брезенхейма для построения окружностей.
Процедура построения прямой соответствует коду соответствующей статьи, но имеет заголовок
Procedure line(x1,y1,x2,y2: Integer; ln: Integer = 0; fill: Boolean = False);
В коде присутствует вызов процедуры putpixel(x, y, color), которая закрашивает пиксель (x,y) в цвет color. Нужно сделать установку цвета глобальной в переменную curColor перед запуском процедуры line, а в саму процедуру использовать в формате putpixel(x, y, ln, fill). Код должен выглядеть так:
Procedure putPixel(x,y: Integer; ln: Integer = 0; fill: Boolean = False); var len: Integer; begin Form1.PaintBox1.Canvas.Pixels[x,y]:=curColor; if (fill=True) then begin len:=Length(map[x]); SetLength(map[x],len+1); map[x,len]:=Point(y,ln); end; end;
Здесь добавилось условие, что в случае, когда необходимо закрасить многоугольник, мы для столбца x в глобальный массив map записываем новую точку. Массив map задаётся как map: array [0..500] of array of TPoint, где [0,500] — размеры экрана рисования. В качестве значения для нового элемента массива ставим пару чисел (значение ординаты, номер прямой в массиве). Таким образом мы сможем обрабатывать порядок прямых в спорных ситуациях. Само множество вершин многоугольника хранится в массиве figure.
После построения всех сторон многоугольника получаем заполненный массив map, содержащий все точки, находящиеся на границе многоугольника. Теперь нужно отсортировать для каждой вертикали xi все точки, принадлежащие этой вертикали. Ниже приведён код сортировки.
Procedure lineSort(index: Integer); var i,j,k,l,A,B,C,D: LongInt; fl: Double; deep: Array of Double; arr: Array [0..500] of Array of Integer; x,y,z: TPoint; begin //сортировка подсчётом for i:=500 downto 0 do begin SetLength(arr[i],0); end; for i:=Length(map[index])-1 downto 0 do begin j:=Length(arr[map[index][i].x]); Setlength(arr[map[index][i].x],j+1); arr[map[index][i].x][j]:=map[index][i].y; end; l:=Length(figure); for k:=500 downto 0 do begin if (Length(arr[k])>1) then begin //проверка порядка точек на одном пикселе SetLength(deep,Length(arr[k])); for i:=Length(arr[k])-1 downto 0 do begin if (l>0) then begin A:=figure[arr[k,i]-1].y-figure[arr[k,i] mod l].y; B:=figure[arr[k,i] mod l].x-figure[arr[k,i]-1].x; C:=-A*figure[arr[k,i]-1].x-B*figure[arr[k,i]-1].y; if (B<>0) then begin deep[i]:=(A*index+C+0.0)/(-B+0.0); end else begin deep[i]:=k; end; end else begin deep[i]:=k; end; end; //сортировка for i:=length(arr[k])-1 downto 1 do begin for j:=i-1 downto 0 do begin if (deep[i]>deep[j]) then begin //если на разной высоте D:=arr[k,i]; arr[k,i]:=arr[k,j]; arr[k,j]:=D; fl:=deep[i]; deep[i]:=deep[j]; deep[j]:=fl; end else if (deep[i]=deep[j]) and (l>0) then begin //если равны и это не круг if (arr[k,i]<arr[k,j]) and ((arr[k,j]<>Length(figure)) or (arr[k,i]<>1)) then begin x:=figure[arr[k,i]-1]; y:=figure[arr[k,j] mod l]; z:=figure[arr[k,i]]; end else begin x:=figure[arr[k,i] mod l]; y:=figure[arr[k,j]-1]; z:=figure[arr[k,j] mod l]; end; A:=z.y-x.y; B:=abs(x.x-z.x); C:=z.y-y.y; D:=abs(y.x-z.x); if ((D=0) and (C>0)) or ((A<=0) and (C>0)) or ((A<0) and (C=0)) or ((A>0) and (C>0) and (B*C>A*D)) or ((A<0) and (C<0) and (B*C>A*D)) then begin D:=arr[k,i]; arr[k,i]:=arr[k,j]; arr[k,j]:=D; end; end; end; end; end; end; i:=0;j:=0; for k:=0 to 500 do begin if (Length(arr[k])>0) then begin for i:=Length(arr[k])-1 downto 0 do begin map[index,j]:=Point(k,arr[k][i]); Inc(j); end; end; end; end;
Сначала происходит сортировка подсчётом с использованием динамического массива для каждой ординаты. Таким образом мы упорядочиваем все точки с данной координатой xi по возрастанию значения y. Далее идёт дополнительная сортировка для тех значений, где в один пиксель попадает несколько рёбер. Такая ситуация возможна в двух случаях:
- в вершинах многоугольника соединяются два ребра с соседними номерами;
- за счёт перехода к целочисленным координатам при работе алгоритма Брезенхейма (Рис. 1).
![]()
Рис. 1
Порядок рёбер в данном пикселе определяется через построение уравнения прямой для конкретного ребра (опускается при обработке круга) и подстановки туда значения xi, тем самым можно получить реальное значение yj, в котором ребро j пересекает xi. Гарантируется, что прямая, на которой лежит ребро, имеет хотя бы одну точку пересечения с прямой x=xi, так как у каждой точки указано, какому ребру она принадлежит, а все координаты вершин целые.
Подстановкой в уравнение вида y=-(Aj*x+Cj)/Bj значения x=xi получаем значение yj. Если же Bj=0 или рассматриваемая фигура — круг, то ставим yj=k (текущая проверяемая ордината). Далее идёт обычная сортировка вставкой, упорядочивающая точки по возрастанию реальной yj. Если встречаются две точки P(xi, yp) и S(xi, ys) такие, что yp=ys, то это возможно лишь когда P и S — вершина многоугольника, полученная от двух соседних рёбер. Тогда нужно определить, в какую сторону происходит перегиб. Для этого рассмотрим дополнительно две вершины, соседних с данной. Если у «исходящего» ребра угол меньше, чем у «входящего», то их нужно поменять. Угол определяется между ребром и отрезком (P,O), где O=(xi, 500).
В конце алгоритма сортировки нужно перенести обработанный массив обратно в соответствующий map[xi], выставив его снова в убывающем порядке.
Теперь нужно провести дальнейшую нормировку множества точек, основываясь на полученной сортировке. Рассмотрим тривиальный случай для круга, построенного по алгоритму из статьи. Здесь круг рисуется восемью линиями, но мы будем их обозначать четырьмя номерами согласно четвертям координатной плоскости, в которых лежит линия относительно центра круга. Так как точки выставляются симметрично, то при сортировке достаточно просто упорядочить все точки по ординате. Закрашивается та часть, которая находится между двумя средними точками в массиве. Если их ординаты совпадают или в массиве нечётное число элементов, то значит закрашивание не требуется, иначе просто оставим только две точки вокруг середины массива.
Procedure figureNorm(xMin,xMax: Integer); var i,j,x,y,l: Integer; upPoint,leftPoint: Boolean; begin for i:=xMin to xMax do begin lineSort(i); //сортировка end; l:=Length(figure); for i:=l-1 downto 0 do begin x:=figure[(i+1) mod l].x; y:=figure[(i-1+l) mod l].x; x:=x-figure[i].x; y:=y-figure[i].x; if ((x>0) and (y>0)) or ((x<0) and (y<0)) then begin //рёбра по одну сторону от вертикали (11 и 12) end else if ((x<0) and (y>0)) or ((x>0) and (y<0)) then begin //рёбра по разную сторону, «перегиб» (10) deleteLine(figure[i].x,i); end else if (x=0) and (y=0) then begin //невозможно, чтобы лежали на одной прямой!!! (1) end else begin //одно из рёбер вертикальное upPoint:=False; leftPoint:=False; if (x=0) then begin //«исходящее» ребро вертикально j:=i+1; if (figure[(i+1) mod l].y<figure[i].y) then begin upPoint:=True; end; if (y<0) then begin leftPoint:=True; end; deleteLine(figure[i].x,i); end else begin //«входящее» ребро вертикально j:=i; if (j=0) then j:=l; //вместо ребра с номером 0 надо взять номер N if (figure[(i-1+l) mod l].y<figure[i].y) then begin upPoint:=True; end; if (x<0) then begin leftPoint:=True; end; deleteLine(figure[i].x,i+1); end; if (upPoint=true) then begin if (leftPoint=true) then begin //5 и 9 deletePoint(figure[i].x,figure[i].y,j,-4); end else begin //4 и 8 deletePoint(figure[i].x,figure[i].y,j,-3); end; end else begin if (leftPoint=true) then begin //3 и 7 deletePoint(figure[i].x,figure[i].y,j,-1); end else begin //2 и 6 deletePoint(figure[i].x,figure[i].y,j,-2); end; end; end; end; end;
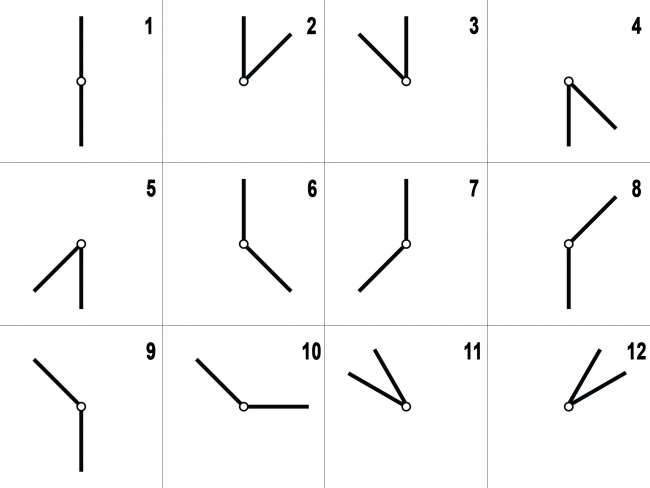
Рис. 2
Теперь рассмотрим случай для многоугольника. Пройдём по всем вершинам многоугольника и проверим, какого формата там пересечение (Рис. 2). Так как удалять из динамического массива информацию затратно, то используются две псевдоудаляющие процедуры: deletePoint заменяет номер указанного ребра в массиве map[xi] на указанное значение, а deleteLine полностью удаляет из map[xi] все вхождения указанного ребра. Так как рёбра имеют номера [1,N], то при удалении через deleteLine ставится 0, а при замене через deletePoint — отрицательные числа.
Завершающей процедурой является сама заливка. Разберём её код, представленный ниже.
Procedure runFill(xMin,xMax: Integer); var i,j,vert,prev,lowest: Integer; draw,vertDraw: Byte; lines: array of Integer; adding: Boolean; begin for i:=xMin to xMax do begin draw:=0; vert:=0; lowest:=0; vertDraw:=0; SetLength(lines,0); j:=Length(map[i])-1; prev:=Form1.PaintBox1.Canvas.Height-1; adding:=False; while (j>=0) do begin if (prev>map[i,j].x) then begin //есть пустое место if ((Length(lines)-lowest) mod 2=1) then begin draw:=1-draw; end; lowest:=Length(lines); if (draw=1) and (vert=0) then begin //закрашиваем, если можно while (prev>map[i,j].x) do begin putPixel(i,prev); Dec(prev); end; end else begin prev:=map[i,j].x; end; end; while (j>=0) and (map[i,j].x=prev) do begin //все точки с текущей ординатой if (map[i,j].y<0) then begin //вертикальное ребро if (vert=0) then begin //запоминаем режим рисования vertDraw:=draw; vert:=map[i,j].y; end else begin //конец ребра — восстанавливаем режим if (map[i,j].y+vert=-5) then begin draw:=vertDraw; end else begin draw:=1-vertDraw; end; vertDraw:=0; vert:=0; lowest:=Length(lines); end; end else if (map[i,j].y>0) then begin if (adding=False) then begin while (lowest<Length(lines)) and (map[i,j].y<>lines[lowest]) do begin //часть нижних рёбер могла закончится Inc(lowest); draw:=1-draw; end; end; if (lowest=Length(lines)) or (adding=True) then begin //добавляем новые рёбра adding:=True; SetLength(lines,Length(lines)+1); lines[Length(lines)-1]:=map[i,j].y; end; end; Dec(j); end; adding:=False; Dec(prev); end; SetLength(map[i],0); //очищаем массив end; end;
В данном коде используется следующая схема: проходим по всем точкам, принадлежащим рёбрам. Если от предыдущей точки до проверяемой есть незакрашенные точки, то если режим draw=1, и при этом сейчас не вертикальная линия, то закрашиваем промежуток, иначе просто пропускаем. В массиве lines хранятся номера рёбер, которые уже начались, а lowest указывает в этом массиве на тот элемент, где хранится текущий блок рёбер и lines[lowest] имеет самое большое значение y среди всех рёбер, проходящих через этот пиксель. Ребро считается начавшимся тогда, когда по данной вертикали имеет более одного пикселя, и самый верхний пиксель уже рассмотрен. Если у нас был пустой блок пикселей, то ещё нужно сменить режим рисования согласно количеству «открытых» рёбер (лежащих в массиве).
Далее проверяются все точки с одинаковой ординатой. Если началось вертикальное ребро, то запоминаем режим рисования и игнорируем все дальнейшие точки до тех пор, пока не встретим конец вертикали. Эти два события определяются благодаря тому, что на концах вертикали устанавливаются отрицательные числа. Выбор отрицательных чисел сделан таким образом, чтобы в сумме на концах вертикального ребра получалось -5, если по его окончанию нужно продолжить режим закрашивания, который был до начала ребра, иначе режим меняется на противоположный.
Если же ребро обычное, то проверяем записанные в lines номера рёбер и те, которые указаны для текущей ординаты. Так как в обоих случаях массивы упорядочены по реальному значению yj для ребра, то если одно ребро занимает два соседних пикселя, то в обоих случаях оно будет идти одинаково отсортированным относительно других рёбер. Если первые рёбра в lines и в массиве для текущей ординаты не совпадают, значит часть рёбер, лежащих в lines, закончилась, а потому нужно их убрать из списка (увеличить lowest) и изменить режим рисования на противоположный за каждое закончившееся ребро. Если lines опустел (lowest = Length(lines)) или начались новые рёбра, то записываем их в массив lines.
Пример работы программы:
| Прикрепленный файл | Размер |
|---|---|
| algo.zip | 730.03 кб |




