Расстояние между отрезками

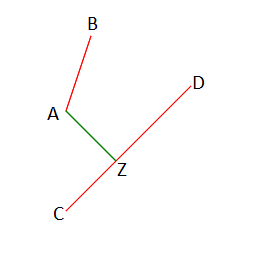
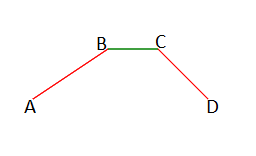
Координаты концов первого отрезка: A(x_a, y_a), B(x_b, y_b).
Координаты концов второго отрезка: C(x_c, y_c), D(x_d, y_d).

Для начала проверим не пересекаются ли отрезки.
Пусть для отрезка AB: x = t(x_b - x_a) + x_a, y = t(y_b - y_a) + y_a, тогда для CD: x = s(x_d - x_c) + x_c, y = s(y_d - y_c) + y_c, где 0 ≤ t,s ≤ 1.

Если отрезки пересекаются, то выполняются равенства:
t(x_b - x_a) - s(x_d - x_c) = x_c - x_a и t(y_b - y_a) - s(y_d - y_c) = y_c - y_a.

Полученную систему уравнений решим методом Крамера:
Δ = (x_b - x_a)(y_с - y_d) - (y_b - y_a)(x_с - x_d).
Δ₁ = (x_b - x_a)(y_с - y_a) - (y_b - y_a)(x_с - x_a).
Δ₂ = (x_c - x_a)(y_с - y_d) - (y_c - y_a)(x_с - x_d).

Тогда t = Δ₁/Δ, s = Δ₂/Δ. Если 0 ≤ t,s ≤ 1 и Δ ≠ 0, то отрезки пересекаются и расстояние между ними min равно 0, иначе с каждого конца отрезка попытаемся опустить высоту на противоположный. Если отрезок, на который опускаем высоту вертикальный, то поменяем местами координаты каждого конца отрезка и точки, с которой опускаем высоту (таким образом сохраним расстояние между точкой и отрезком, а отрезок станет горизонтальным).

Пусть k и d — коэффициенты уравнения прямой, на которую опущена эта высота. Основание высоты будет находится на прямой в точке Z, координаты Z(x_z, y_z) можно найти по формуле y_z = kx_z + d. Поскольку высота перпендикулярна отрезку — скалярное произведение их векторов равно 0. Тогда (x₂ - x₁)(x₃ - x_z)+(y₂ - y₁)(y₃ - y_z) = 0, соответственно x_z = (x₃x₂ - x₃x₁ + y₂y₃ - y₁y₃ + y₁d - y₂d)/(ky₂ - ky₁ + x₂ - x₁), где (x₃, y₃) — координаты точки, с которой была опущена высота, (x₁, y₁) и (x₂, y₂) — координаты концов отрезка, принадлежащего прямой на которую опущена высота.

Вычислим длину dl каждой высоты, основание которой принадлежит одному из данных отрезков: dl = √((x₃ - x_z)² + (y₃ - kx_z - d)²).

Минимальная длина высоты и будет наименьшим расстоянием между отрезками. В случае, если невозможно опустить высоты из одного отрезка на другой: расстояние между ними будет равно минимальному расстоянию между концами двух отрезков: min = √((x₁ - x₃)² + (y₁ - y₃)²), где (x₁, y₁) — координаты одного из концов первого отрезка, а (x₃, y₃) — координаты одного из концов второго отрезка.