Среда программирования:
JavaScript
Статья по теме:
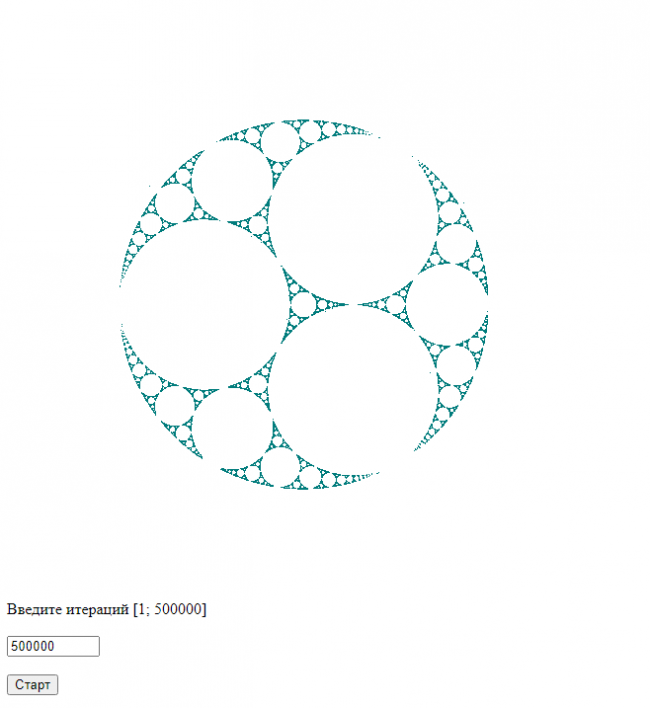
Данная программа получает на вход кол-во итераций от пользователя и строит Аполлониево множество.
Код программы:
var ctx, imgData, canvas; var color = {r: 0, g: 124, b: 124 , a: 255}; canvas = document.getElementById("cnvs"); ctx = canvas.getContext("2d"); function setPixel(x, y, c) { /* Устанавливает пиксель с координатой (x, y) с цветом c */ var index = 4 * (x + canvas.width * y); // получаем индекс пикселя imgData.data[index + 0] = c.r; imgData.data[index + 1] = c.g; imgData.data[index + 2] = c.b; imgData.data[index + 3] = c.a; return c; } function drawFractal(iter) { /* Итеративная функция для рисования Аполлониева множества. Вход: число итераций */ var x = 0.2, y = 0.3; var a = 0.0, b = 0.0; var r = Math.sqrt(3), i = 0; while(i < iter) { a = Math.random(); a0 = 3 * (1 + r - x) / (Math.pow(1 + r - x, 2) + Math.pow(y, 2)) - (1 + r) / (2 + r); b0 = 3 * y / (Math.pow(1 + r - x, 2) + Math.pow(y, 2)); if ((a <= 1/3) && (a >= 0)) { x1 = a0; y1 = b0; } a1 = -0.5, b1 = r / 2, a2 = -0.5, b2 = -r / 2; f1x = a0 / (Math.pow(a0, 2) + Math.pow(b0, 2)); f1y = -b0 / (Math.pow(a0, 2) + Math.pow(b0, 2)); if ((a <= 2 / 3) && (a > 1 / 3)) { x1 = f1x * a1 - f1y * b1; y1 = f1x * b1 + f1y * a1; } if ((a <= 1) && (a > 2 / 3)) { x1 = f1x * a2 - f1y * b2; y1 = f1x * b2 + f1y * a2; } x = x1, y = y1; setPixel(300 + Math.round(x * 50), 300 + Math.round(y * 50), color); i++; } } function draw() { var iter = Math.min(500000, document.getElementById("iterationCnt").value); imgData = ctx.createImageData(600, 600); ctx.putImageData(imgData, 0, 0); drawFractal(iter); // вызываем функцию отрисовки ctx.putImageData(imgData, 0, 0); }
| Прикрепленный файл | Размер |
|---|---|
| apollon_set.zip | 13.46 кб |




