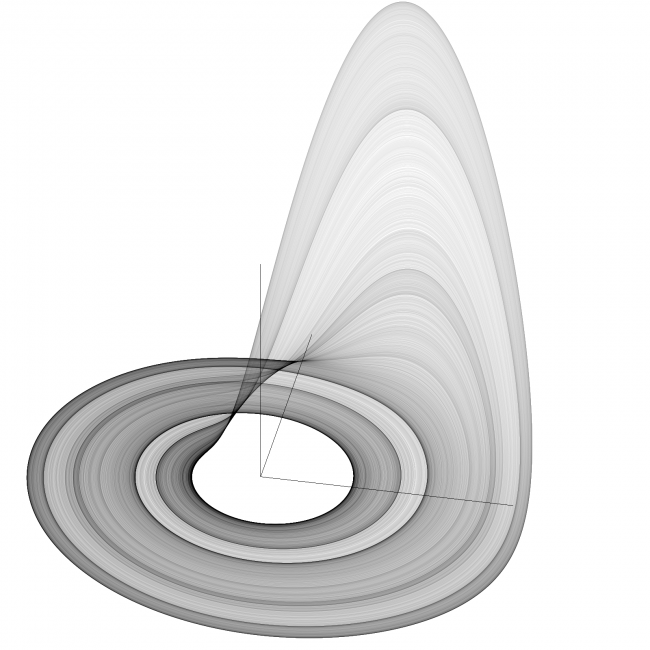
Аттрактор Рёсслера — хаотический аттрактор, которым обладает система дифференциальных уравнений Рёсслера:
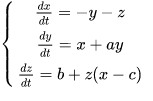
где a, b, c — положительные постоянные. При значениях параметров a = b = 0.2 и 2.6 < c < 4.2 уравнения Рёсслера обладают устойчивым предельным циклом. При этих значениях параметров в системе происходит каскад удвоения периода. При c > 4.2 возникает хаотический аттрактор. Чётко определённые линии предельных циклов расплываются и заполняют фазовое пространство бесконечным множеством траекторий, обладающим свойствами фрактала. Сам Рёсслер изучал систему при постоянных a = 0.2, b = 0.2, c = 5.7.
Когда 0 < a < 2, собственные значения имеют положительную вещественную часть и комплексно сопряжены. Поэтому фазовые траектории расходятся от начала координат по спирали. Теперь проанализируем изменение координаты z, считая 0 < a < 2. Пока x меньше c, множитель x - c в уравнении на dz / dt будет удерживать траекторию близкой к плоскости x, y. Как только x станет больше c, z-координата начнёт расти. В свою очередь, большой параметр z начнёт тормозить рост x в dz / dt.
Поведение аттрактора Рёсслера сильно зависит от значений постоянных параметров. Изменение каждого параметра даёт определённый эффект, в результате чего в системе может возникнуть устойчивая неподвижная точка, предельный цикл или решения системы станут "убегать" на бесконечность.




