Системы синтеза реалистических изображений должны обеспечивать передачу всех свойств моделируемого объекта: объемность, расположение, передачу полутонов, тени, освещение, текстуры поверхности. Чем выше степень реалистичности изображения, тем больше требуется вычислений для его формирования.
Генерация объемных изображений представляет сложную вычислительную задачу, в связи этим на практике выполняют ее декомпозицию. Сложные изображения формируют из фрагментов объектов, для чего их разбивают на составные части. Процесс разбиения поверхности объектов на полигоны получил название тесселяции.
В настоящее время появилось большое разнообразие графических акселераторов, которые имеют различные аппаратные графические функции для закраски трехмерных объектов, удаления невидимых частей, наложения текстур и т.п. Для использования преимуществ 3D-ускорителей необходимо сначала программно произвести тесселяцию исходных объектов, а затем передать полученные полигональные области для дальнейшей обработки акселератору.
На практике наиболее часто производится разбиение изображений на треугольники.
Это объясняется следующими причинами:
• треугольник является простейшим полигоном, вершины которого однозначно задают грань;
• любую область можно гарантировано разбить на треугольники;
• вычислительная сложность алгоритмов разбиения на треугольники существенно меньше, чем при использовании других полигонов;
• реализация процедур рендеринга наиболее проста для области, ограниченной треугольником;
• для треугольника легко определить три его ближайших соседа, имеющих с ним общие грани.
Процесс разбиения полигональной области со сложной конфигурацией в набор треугольников называется триангуляцией. При анализе или синтезе сложных поверхностей их аппроксимируют сеткой треугольников, и впоследствии оперируют с простейшими полигональными областями, т.е. с каждым из треугольников.
Алгоритм триангуляции:
1. Берем три вершины A1, A2, A3
2. Проверяем образуют ли вектора A1A3, A1A2 и их векторное произведение левую тройку векторов.
3. Проверяем нет ли внутри треугольника A1A2A3 какой-либо из оставшихся вершин многоугольника.
4. Если оба условия выполняются, то строим треугольник A1A2A3, а вершину A2 исключаем из многоугольника, не трогая вершину A1, сдвигаем вершины A2 (A2 на A3), A3 (A3 на A4)
5. Если хоть одно условие не выполняется, переходим к следующим трем вершинам.
6. Повторяем с 1 шага, пока не останется три вершины.
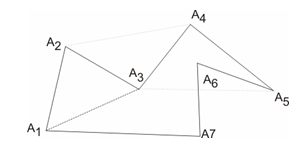
Рис.1 Алгоритм триангуляции невыпуклого многоугольника
На рисунке 1
• треугольник A1A2A3 удовлетворяет обоим условиям (п.2, п.3);
• треугольник A2A3A4 не удовлетворяет условию (п.2);
• треугольник A3A4A5 не удовлетворяет условию (п.3).




