
Семейство Т-фракталов было впервые описано в 1977 году Бенуа Мандельбротом в своей книге «Фрактальная геометрия природы». Основной особенностью этого семейства является наличие образа буквы "Т".
В основе этого семейства лежат вариации построения Т-квадрата.
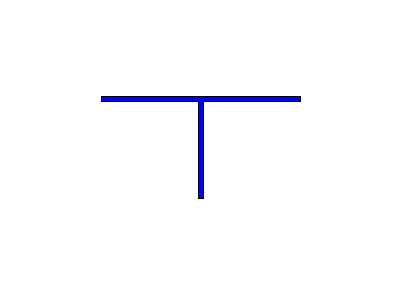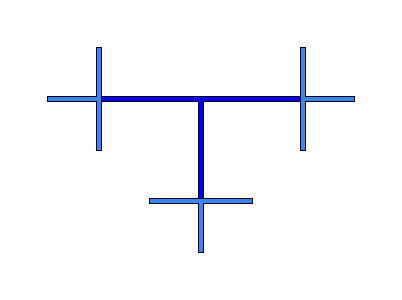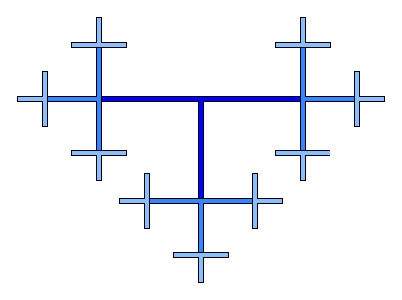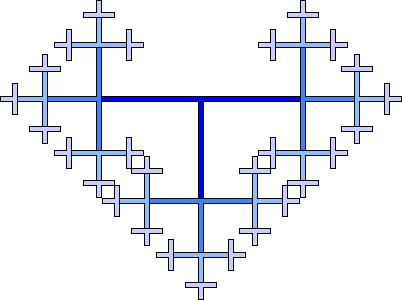
Построение начинается с синего единичного квадрата. Первый шаг: закрасить в центре белым цветом квадрат со стороной 1/2. Затем нужно мысленно разделить квадрат на 4 одинаковых квадрата и в центре каждого из них закрасить квадрат со стороной 1/4. Дальше каждый из этих 4 квадратов снова делится на 4 части, всего получится 16 квадратиков, и с каждым из них нужно проделать то же самое. И так далее.
Свойства Т-квадрата:Фрактальная размерность закрашенной белым в конце концов части равна log24 = 2. Она всюду плотна в исходном квадрате. Это означает, что какую бы точку квадрата мы ни взяли, в любой, сколь угодно малой, ее окрестности найдутся закрашенные точки. То есть в итоге почти всё стало белым — площадь остатка равна 0, а фрактал занимает площадь 1. Зато длина границы закрашенной части бесконечна.




