Алгоритм Брезенхема для генерации окружности

См. исправленный алгоритм Брезенхема построения окружности здесь https://cgraph.ru/node/308

Во многих областях приложений, таких как, например, системы автоматизированного проектирования машиностроительного направления, естественными графическими примитивами, кроме отрезков прямых и строк текстов, являются и конические сечения, т.е. окружности, эллипсы, параболы и гиперболы. Наиболее употребительным примитивом, естественно, является окружность. Один из наиболее простых и эффективных алгоритмов генерации окружности разработан Брезенхемом.

Алгоритм Брезенхема

Для простоты и без ограничения общности рассмотрим генерацию 1/8 окружности, центр которой лежит в начале координат. Остальные части окружности могут быть получены последовательными отражениями (использованием симметрии точек на окружности относительно центра и осей координат).

Окружность с центром в начале координат описывается уравнением:

X² + Y² = R²

Алгоритм Брезенхема пошагово генерирует очередные точки окружности, выбирая на каждом шаге для занесения пиксела точку растра P_i(X_i, Y_i), ближайшую к истинной окружности, так чтобы ошибка:

E_i(P_i) = (X_i² + Y_i²) - R²

была минимальной. Причем, как и в алгоритме Брезенхема для генерации отрезков, выбор ближайшей точки выполняется с помощью анализа значений управляющих переменных, для вычисления которых не требуется вещественной арифметики. Для выбора очередной точки достаточно проанализировать знаки.

Рассмотрим генерацию 1/8 окружности по часовой стрелке, начиная от точки X=0, Y=R.

Проанализируем возможные варианты занесения i+1-й точки, после занесения i-й.

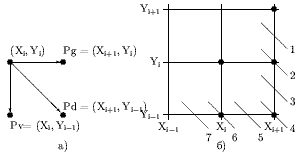
При генерации окружности по часовой стрелке после занесения точки (X_i, Y_i) следующая точка может быть (см. рис. 0.1а) либо Pg = (X_i+1, Y_i) - перемещение по горизонтали, либо Pd = (X_i+1, Y_i-1) - перемещение по диагонали, либо Pv = (X_i, Y_i-1) - перемещение по вертикали.

Для этих возможных точек вычислим и сравним абсолютные значения разностей квадратов расстояний от центра окружности до точки и окружности:

|Dg| =| (X+1)²+Y²-R² |
|Dd|=| (X+1)²+(Y-1)²-R² |
|Dv|=| X²+(Y-1)²-R² |

Выбирается и заносится та точка, для которой это значение минимально.

Выбор способа расчета определяется по значению Dd. Если Dd < 0, то диагональная точка внутри окружности. Это варианты 1-3 (см. рис. 0.1б). Если Dd > 0, то диагональная точка вне окружности. Это варианты 5-7. И, наконец, если Dd = 0, то диагональная точка лежит точно на окружности. Это вариант 4. Рассмотрим случаи различных значений Dd в только что приведенной последовательности.

Случай Dd < 0

Здесь в качестве следующего пиксела могут быть выбраны или горизонтальный - Pg или диагональный - Pd.

Для определения того, какой пиксел выбрать Pg или Pd составим разность:

di = |Dg| - |Dd| = |(X+1)² + Y² - R²| - |(X+1)² + (Y-1)² - R²|
И будем выбирать точку Pg при di <= 0, в противном случае выберем Pd.

Рассмотрим вычисление di для разных вариантов.

Для вариантов 2 и 3:

Dg >= 0 и Dd < 0, так как горизонтальный пиксел либо вне, либо на окружности, а диагональный внутри.

di = (X+1)² + Y² - R² + (X+1)² + (Y-1)² - R²;
Добавив и вычтя (Y-1)² получим:

di = 2 ·[(X+1)² + (Y-1)² - R²] + 2·Y - 1
В квадратных скобках стоит Dd, так что

di = 2 ·(Dd + Y) - 1

Для варианта 1:

Ясно, что должен быть выбран горизонтальный пиксел Pg. Проверка компонент di показывает, что Dg < 0 и Dd < 0, причем di < 0, так как диагональная точка больше удалена от окружности, т.е. по критерию di < 0 как и в предыдущих случаях следует выбрать горизонтальный пиксел Pg, что верно.

Случай Dd > 0

Здесь в качестве следующего пиксела могут быть выбраны или диагональный - Pd или вертикальный Pv.

Для определения того, какую пиксел выбрать Pd или Pv составим разность:

si = |Dd| - |Dv| = |(X+1)² + (Y-1)² - R²| - |X² + (Y-1)² - R²|
Если si <= 0, то расстояние до вертикальной точки больше и надо выбирать диагональный пиксел Pd, если же si > 0, то выбираем вертикальный пиксел Pv.

Рассмотрим вычисление si для разных вариантов.

Для вариантов 5 и 6:

Dd > 0 и Dv <= 0, так как диагональный пиксел вне, а вертикальный либо вне либо на окружности.

si = (X+1)² + (Y-1)² - R² + X² + (Y-1)² - R²;
Добавив и вычтя (X+1)² получим:

si = 2 ·[(X+1)² + (Y-1)² - R²] - 2·X - 1
В квадратных скобках стоит Dd, так что

si = 2 ·(Dd - X) - 1

Случай Dd = 0

Для компонент di имеем: Dg > 0 и Dd = 0, следовательно по критерию di > 0 выбираем диагональный пиксел.

С другой стороны, для компонент si имеем: Dd = 0 и Dv < 0, так что по критерию si <= 0 также выбираем диагональный пиксел.

Итак:

Dd < 0

di <= 0 - выбор горизонтального пиксела Pg

di > 0 - выбор диагонального пиксела Pd

Dd > 0

si <= 0 - выбор диагонального пиксела Pd

si > 0 - выбор вертикального пиксела Pv

Dd = 0

выбор диагонального пиксела Pd.

Выведем рекуррентные соотношения для вычисления Dd для (i+1)-го шага, после выполнения i-го.

1. Для горизонтального шага к X_i+1, Y_i

   X_i+1 = X_{i + 1}
   Y_i+1 = Y_i
   Dd_i+1 = (X_i+1+1)² + (Y_i+1-1)² - R² =
   X_i+1² + 2·X_i+1 + 1 + (Y_i+1-1)² - R² =
   (X_i+1)² + (Y_i-1)² - R² + 2·X_i+1 + 1 =
   Ddi + 2·X_i+1 + 1

2. Для диагонального шага к X_i+1, Y_i-1

   X_i+1 = X_{i + 1}
   Y_i+1 = Y_{i - 1}
   Dd_i+1 = Dd_{i + 2} ·X_i+1 - 2 ·Y_i+1 + 2

3. Для вертикального шага к Xi, Y_i-1

   X_i+1 = X_i
   Y_i+1 = Y_{i - 1}
   Dd_i+1 = Dd_i - 2 ·Y_i+1 + 1