Интерполяция полиномом Лангранжа

Определение интерполяции

Интерполяция — в вычислительной математике это способ нахождения промежуточных значений величины по имеющемуся дискретному набору известных значений.
Задача: по заданному набору точек на плоскости необходимо построить график функции, проходящий через эти точки.

Существует несколько способов решения этой задачи. Способ представленный в этой статье называется интерполяцией с помощью многочлена Лангранжа (интерполяционный многочлен).

Жозеф Луи Лангранж

Жозеф Луи Лангранж - французский математик, астроном и механик итальянского происхождения. Наряду с Эйлером — крупнейший математик XVIII века.
Много своего времени он посвящал обобщению и синтезу уже известных научных открытий.

В 1795 году: открылась Нормальная школа, и Лагранж преподаёт там математику. В 1797 году, после создания Политехнической школы, вёл там преподавательскую деятельность, читал курс математического анализа.

В эти годы Лагранж публикует свою знаменитую интерполяционную формулу для приближения функции многочленом. Издаёт книгу «Теория аналитических функций», без актуальных бесконечно малых. Эта работа позже вдохновляла Коши при разработке строгого обоснования анализа. Там же Лагранж дал формулу остаточного члена ряда Тейлора, указал метод множителей Лагранжа для решения задач на условный экстремум.

Под статьей прикреплена ссылка на файл биографии Жозефа Луи Лангранжа.

Интерполяцио́нный многочле́н Лагра́нжа

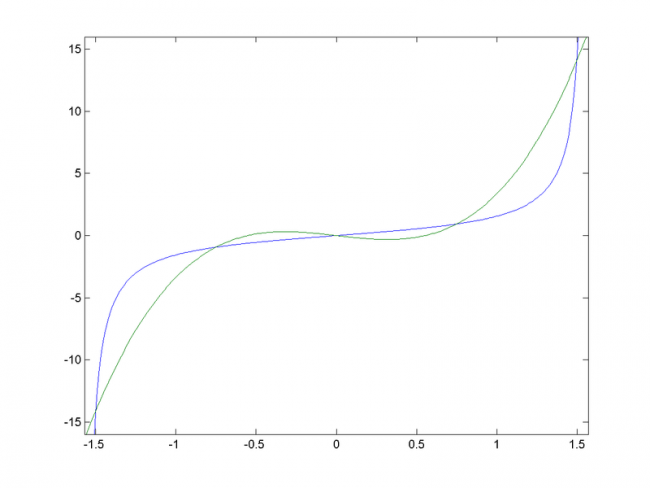
Функция тангенса и рядом интерполяция некоторому по набору точек, удовлетворяющих уравнению этой функции. Графики немного отличаются из-за погрешности при вычислении полинома Лангранжа

Интерполяцио́нныйй многочлен Лангранжа — это многочлен минимальной степени, принимающий данные значения в данном наборе точек. Для n+1 пар чисел (x₀, y₀), (_x1, y₁),…, (x_n, y_n), где все x_j различны, существует единственный многочлен L(x) степени не более n, для которого L(x_j) = y_j.

В простейшем случае (n = 1) — это линейный многочлен, график которого — прямая, проходящая через две заданные точки.

Давайте запишем формулу, по которой можно вычислить этот полином, имея заданный набор точек.

L(x) = ∑y_il_i(x), 1 <= i <= n , где y _i - это y координата i-ой точки, т.е. значение функции, которую нам нужно найти, в точке x_i, а l_i(x) - i-ый базисный полином.

Базисные полиномы вычисляются по формуле:

l_i = Π (x-x_j)/(x_i-x_j), 1 <= j <= n, j ≠ i П - знак произведения по всем j, удовлетворяющим заданным условиям. x_i, x_j - координата x i-ой и j-ой точек соответственно.

l_i(x) обладают следующими свойствами:

являются многочленами степени n
l_i(x_i) = 1
l_i(x_j) = 0 при j ≠ i
Отсюда следует, что L(x), как линейная комбинация l_i(x), может иметь степень не больше n, и L(x_i) = y_i.

Из формулы l_i = Π (x-x_j)/(x_i-x_j), 1 <= j <= n, j ≠ i Мы видим, что многочлен Лангранжа можно построить итеративно по определению.

Для этого, напишем функцию вычисления координаты y для каждого x из области определения. x_min <= x <= x_max

x_min = min(x_i) i = [1, n]
x_max = max(x_i) i = [1, n]

Схема Эйткена

Существуют еще один способ построения этого полезного многочлена: с помощью схемы Эйткена.

Схема Эйткена — это итерационный способ вычисления интерполяционного многочлена Лагранжа, который позволяет за квадратичное относительно количества узлов интерполяции время добавлять в многочлен информацию о новых точках.

Пусть P_left...right(x) обозначим многочлен Лангранжа, построенный на точках (x_left, y_left), (x_left+1, y_left+1), (x_left+2, y_lef+2), ... (x_right, y_right).

Существует следующая формула:
P_i(x) = y_i (вырожденный случай, многочлен нулевой степени — константа, т.е. когда left = right)

P_left...right(x) = 1\(x_j-x_i) * det((x-x_left)*P_{left+1...right}(x) - (x-x_right)*P_{left...right-1}(x))

Исходя из этого мы можем итеративно построить полином P_1...n(x) для всего набора из n точек.

Если вам интересно, как же получается эта схема, то перейдите по этой ссылке.