Среда программирования:
Lazarus
Статья по теме:
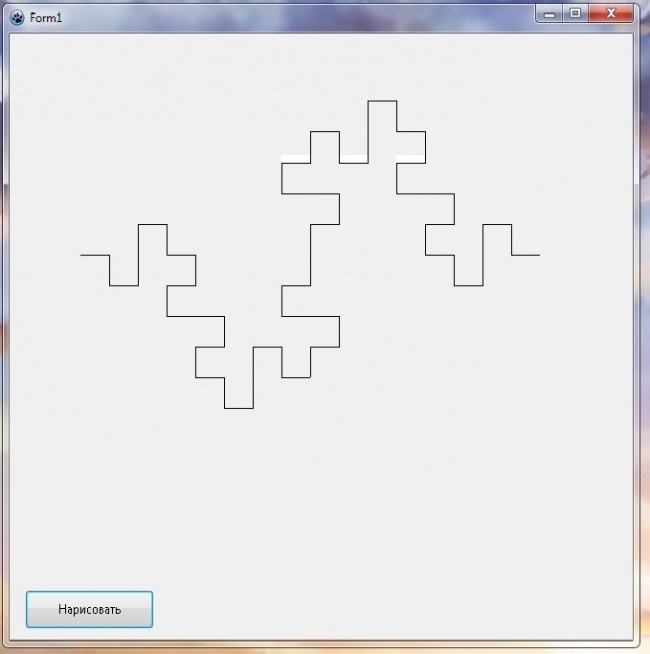
Программа отрисовывает кривую Минковского.
Для запуска программы в левом углу нажимаем на кнопку "Нарисовать".
Код программы:
unit Unit1; {$mode objfpc}{$H+} interface uses Classes, SysUtils, FileUtil, Forms, Controls, Graphics, Dialogs, ExtCtrls, Buttons; type { TForm1 } TForm1 = class(TForm) BitBtn1: TBitBtn; PaintBox1: TPaintBox; procedure BitBtn1Click(Sender: TObject); procedure Gor(x,y: integer); procedure Ver(x,y: integer); procedure Minkovsky(x,y: integer); private { private declarations } public { public declarations } end; var Form1: TForm1; var i,x1,y1,k,n:LongInt; implementation {$R *.lfm} { TForm1 } procedure TForm1.Gor(x,y: integer); // горизонтальный отрезок begin PaintBox1.Canvas.Line(x,y,x+k div 4,y); PaintBox1.Canvas.Line(x+k div 4,y+k div 4,x+k div 4+k div 4,y+k div 4); PaintBox1.Canvas.Line(x+k div 4+k div 4,y-k div 4,x+k-k div 4,y-k div 4); PaintBox1.Canvas.Line(x+k-k div 4,y,x+k,y); PaintBox1.Canvas.Line(x+k div 4,y,x+k div 4,y+k div 4); PaintBox1.Canvas.Line(x+k div 4+k div 4,y+k div 4,x+k div 4+k div 4,y-k div 4); PaintBox1.Canvas.Line(x+k-k div 4,y-k div 4,x+k-k div 4,y); end; procedure TForm1.Ver(x,y: integer); // вертикальный отрезок begin PaintBox1.Canvas.Line(x,y,x,y+k div 4); PaintBox1.Canvas.Line(x, y+k div 4, x-k div 4,y+k div 4); PaintBox1.Canvas.Line(x-k div 4, y+k div 4, x-k div 4,y+k div 4+k div 4); PaintBox1.Canvas.Line(x-k div 4,y+k div 4+k div 4, x+k div 4,y+k div 4+k div 4); PaintBox1.Canvas.Line(x+k div 4, y+k div 4+k div 4, x+k div 4, y+k-k div 4); PaintBox1.Canvas.Line(x+k div 4, y+k-k div 4, x, y+k-k div 4); PaintBox1.Canvas.Line(x, y+k-k div 4,x,y+k); end; procedure TForm1.Minkovsky(x,y: integer); // функция построения кривой begin Gor(x,y); Ver(x+k,y); Gor(x+k,y+k); Ver(x+2*k, y-k); Ver(x+2*k, y1); Gor(x+2*k,y-k); Ver(x+3*k, y-k); Gor(x+3*k, y); end; procedure TForm1.BitBtn1Click(Sender: TObject); begin k:=120; x1:=50; y1:=200; Minkovsky(x1,y1); end; end.
| Прикрепленный файл | Размер |
|---|---|
| Minkovsky.rar | 686.66 кб |





Комментарии
А как можно добавить сюда глубину рекурсии, то есть сложность линии?