Упаковка Лейбница (Аполлониево Множество) впервые была описана в письме Лейбница к де Броссу: "...Представьте себе окружность, а затем впишите в нее еще три окружности наибольшего возможного радиуса, конгруэнтные друг другу: повторите аналогичную операцию с каждой из этих окружностей и с каждым промежутком между ними. А теперь вообразите, что этот процесс продолжен до бесконечности..."
- так впервые была описана конструкция, в последствии названная Бенуа Мандельбротом Упаковкой Лейбница.
Упаковка Лейбница похожа на более известный фрактал - Аполлониеву Сеть. Представляет она собой бесконечное количество окружностей вместе с их предельными точками.
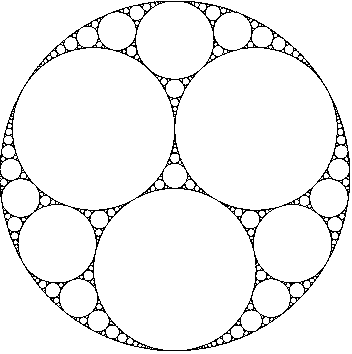
Этот фрактал назван в честь Аполлония Пергского - древнегреческого математика, жившего в III в. до нашей эры. Он был представителем александрийской школы и верным последователем Евклида и известен, помимо прочего, тем, что составил алгоритм построения пяти окружностей, касательных к трем заданным окружностям. В том случае, когда заданные окружности взаимнокасательны , число аполлониевых кругов равно двум.

Совершим переход с плоскости в пространство. Возьмем четыре шара произвольного радиуса, и между ними впишем еще один, далее будем повторять эту процедуру до бесконечности. В итоге мы получим трехмерное Аполлониево Множество. И никто нам не мешает повторить этот процесс с гиперсферами в четырех, пяти и шести мерных пространствах.
Подытожим: множество Аполлона – это вид фрактала, который строится посредством постоянно уменьшающихся в диаметре окружностей в одной большой окружности. Каждая окружность в множестве Аполлона является «касательной» к смежным окружностям, другими словами круги в множестве Аполлона соприкасаются только в бесконечно малой точке.




