Среда программирования:
Emacs
Статья по теме:
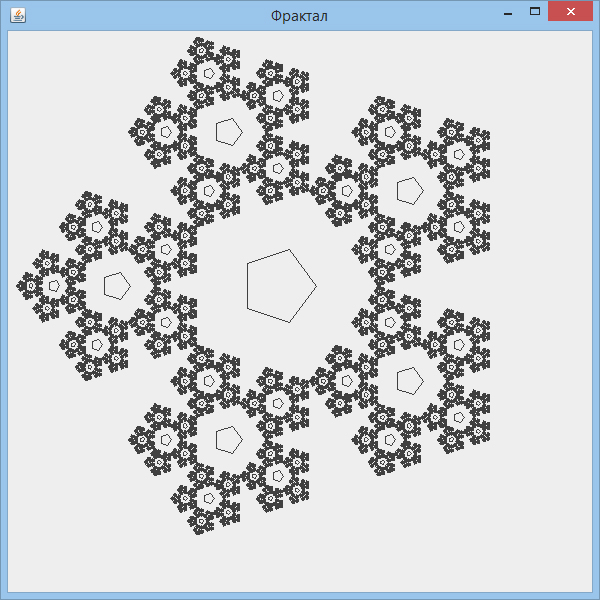
При запуске jar-файла открывается окно, в котором отрисовывается фрактал.
Код программы:
import java.awt.Color; import java.awt.Graphics2D; import javax.swing.JComponent; import javax.swing.JPanel; import java.awt.Graphics; import javax.swing.JFrame; public class Main{ Main(){ JFrame window=new JFrame("Фрактал"); window.setSize(600,600); window.setDefaultCloseOperation(3); window.add(new JComponent() { @Override public void paintComponent(Graphics h){ Graphics2D g=(Graphics2D)h; g.setPaint(Color.DARK_GRAY); func(270,255,100,0,7,g); } void func(double x, double y, double radius,double angle,int deep, Graphics2D g){ /* Для уменьшения кода в строках вводятся эти переменные pi5 равна Пи, делённой на 5 h равна расстоянию от центра большего пятиугольника к центрам меньших */ double pi5=3.141596/5; double h=2*radius*cos(pi5); for(int i=0;i<5;i++){ /* Вычисление некоторых параметров для рисования их на экране ang2 Поворот относительно центрального пятиугольника на 360/5 градусов x2 центр меньшего пятиугольника y2 центр меньшего пятиугольника ang3 уголь, на который нужно повернуть вершину изначально rad расстояние до каждого из углов меньшего пятиугольника от его центра */ double ang2=angle+pi5*i*2, x2=x-h*Math.cos(ang2), y2=y-h*sin(ang2), rad2=radius/(2*cos(pi5)+1), ang3=angle+3.141596+(2*i+1)*pi5; for(int j=0;j<4;j++){ /* В буфер записываются вершины. Эти две вершины будут соединены в прямые между собой*/ g.drawLine((int)(x+rad2*cos(ang3+j*pi5*2)),(int)(y+rad2*sin(ang3+j*pi5*2)) ,(int)(x+rad2*cos(ang3+(j+1)*pi5*2)),(int)(y+rad2*sin(ang3+(j+1)*pi5*2))); } /* Условие выхода из рекурсии. Из максимальной глубины рекурсии не строятся меньшие пятиугольники*/ if(deep>0)func(x2,y2,radius/(2*cos(pi5)+1),angle+3.141596+(2*i+1)*pi5,deep-1, g); } } }); window.setVisible(true); }; protected double cos(double d) { return Math.cos(d); } protected double sin(double ang2) { return Math.sin(ang2); } public static void main(String f[]){new Main();} }
| Прикрепленный файл | Размер |
|---|---|
| DurerJava.zip | 3.3 кб |




