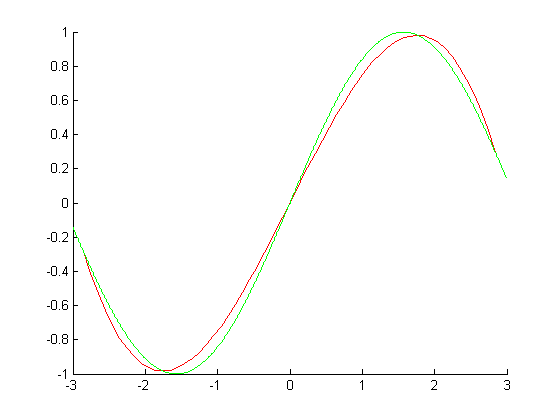
Общий смысл интерполяции
Решение задачи методами интерполирования предполагает выполнение условия P(xi)=f(xi) при x из [a;b] (1)
Интерполяционный алгебраический полином имеет вид Pn(x) = Sum(aixi) где i=0,1,..,n (2)
Задача (1) имеет решение, если степень полинома n = m-1, где m - количество точек интервала [a,b], в которых задана функция f(x). Таким образом, многочлен n-ой степени может обеспечить совпадение с приближаемой функцией f(x) в ( n+1) точке конечного интервала. Однако, поведение разности P(x) - f(x) в точках x из [a;b] и x не равного xi при построении полинома не оговаривается.
Интерполяционный полином в форме Ньютона
Интерполяционный многочлен легко определяется если его построить в виде:
Pn(x) = С0 + С1(x - x0) + C2(x - x0) (x - x1) + ...+ Cn(x - x0)(x - x1) ... (x - xn-1) (5)
Исходя из условия интерполяции (1) для коэффициентов Ci получим систему уравнений треугольного вида
f(x0) = С0
f(x1) = С0 + С1(x1 - x0 )
f(x2) = С0 + С1(x1 - x0 ) + C2(x2 - x0 )(x2 - x1 )
. . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . .
f(xn ) = С0 + С1(xn - x0) + C2(xn - x0)(xn - x1) + ...+ Cn(xn - x0)(xn - x1) ... (xn- xn-1)
Выразив С0, С1, C2 и так далее, мы получим, что величины, стоящие в правой части приведённых равенств, получат название разделённых разностей, соответственно, нулевого, первого, второго, и так далее порядков. Для них приняты обозначения f[xi], f[xi ,xi-1], f[xi ,xi-1 ,xi-2] и т.д. С учётом этих обозначений выражение (5) можно переписать в виде :
Pn(x) = f[x0] + f[x1 ,x0](x - x0) + f[x2 ,x1 ,x0](x - x0)(x - x1) + ...+ f[xn ,xn-1 ,...x0](x - x0)(x - x1)...(x - xn-1) (6)
Выражение (6) определяет интерполяционный полином в форме Ньютона. Вычисление полинома в Ньютоновской форме удобно при последовательном дополнении сетки(n+2)-м узлом и наращивании порядка интерполяционного полинома. При этом необходимо вычислить лишь одно дополнительное слагаемое
f[xn+1 ,xn,...x0](x - x0)(x - x1)...(x - xn) в выражении (6).




