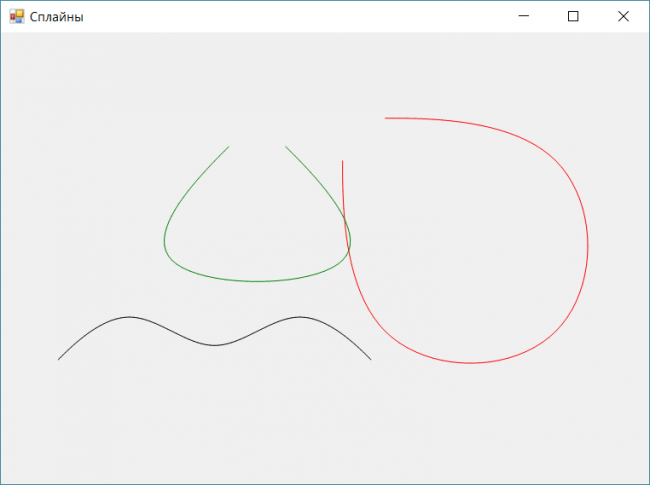
Аппроксимация β-сплайном на C#

using System;
using System.Drawing;
using System.Windows.Forms;
 
namespace WindowsFormsApplication2
{
    public partial class Form1 : Form
    {
        private Bitmap bitmap;
        private Graphics g;
        private Pen pen;
 
        public Form1()
        {
            InitializeComponent();
        }
 
        private void draw()
        {
            pen = new Pen(Color.Black);
 
            int[] spline = new int[] { 50, 400, 150, 300, 250, 400, 350, 300, 450, 400 }; //сплайн - волна
            drawSpline(spline, pen);
 
            spline = new int[] { 400, 100, 700, 100, 700, 400, 400, 400, 400, 100 }; //сплайн по квадрату
            pen.Color = Color.Red;
            drawSpline(spline, pen);
 
            spline = new int[] { 300, 100, 500, 300, 100, 300, 300, 100 }; //сплайн по треугольнику
            pen.Color = Color.Green;
            drawSpline(spline, pen);
 
        }
 
        private void Form1_Load(object sender, EventArgs e)
        {
            bitmap = new Bitmap(panel.Width, panel.Height);
            g = Graphics.FromImage(bitmap);
            g.SmoothingMode = System.Drawing.Drawing2D.SmoothingMode.AntiAlias;
 
            draw();
 
            panel.BackgroundImage = bitmap;
        }
 
        //рисует сплайн по точкам
        public void drawSpline(int[] points, Pen pen)
        {
 
            if (points.Length % 2 == 1 || points.Length < 8) //выходим, если координаты заданы неверно
                return;
 
            drawSpline(points[0], points[1], points[0], points[1], points[2], points[3], points[4],
                       points[5], pen); //рисуем сплайн по первой четверке точек
 
            for (int i = 8; i <= points.Length; i += 2) //рисуем сплайн по каждой четверке точек
                drawSpline(points[i - 8], points[i - 7], points[i - 6], points[i - 5], points[i - 4],
                           points[i - 3], points[i - 2], points[i - 1], pen);
 
            int j = points.Length - 6;
            drawSpline(points[j], points[j + 1], points[j + 2], points[j + 3], points[j + 4],
                       points[j + 5], points[j + 4], points[j + 5], pen); //рисуем сплайн по последней четверкке точек
        }
 
        //сплайн по четырем координатам
        private void drawSpline(int x1, int y1, int x2, int y2, int x3, int y3, int x4, int y4,
                                Pen pen)
        {
            //подсчет коэффициентов сплайна
            float a0 = countSplineCoefficient(0, x1, x2, x3, x4);
            float a1 = countSplineCoefficient(1, x1, x2, x3, x4);
            float a2 = countSplineCoefficient(2, x1, x2, x3, x4);
            float a3 = countSplineCoefficient(3, x1, x2, x3, x4);
 
            float b0 = countSplineCoefficient(0, y1, y2, y3, y4);
            float b1 = countSplineCoefficient(1, y1, y2, y3, y4);
            float b2 = countSplineCoefficient(2, y1, y2, y3, y4);
            float b3 = countSplineCoefficient(3, y1, y2, y3, y4);
 
            float xPrev = a0, yPrev = b0;
 
            for (int i = 1; i <= 20; i++) //разбиваем кривую на 20 отрезков
            {
                float t = i / 20.0f;
                float x = ((a3 * t + a2) * t + a1) * t + a0; //x(t)
                float y = ((b3 * t + b2) * t + b1) * t + b0; //y(t)
 
                g.DrawLine(pen, xPrev, yPrev, x, y); //соединяем подсчитанные точки
                xPrev = x;
                yPrev = y;
            }
        }
 
        //пересчет коэффициентов сплайна
        private float countSplineCoefficient(int index, int x1, int x2, int x3, int x4)
        {
            switch (index)
            {
                case 0:
                    return (x1 + 4 * x2 + x3) / 6.0f; //свободный член
                case 1:
                    return (-x1 + x3) / 2.0f; //коэффициент при t
                case 2:
                    return (x1 - 2 * x2 + x3) / 2.0f; //коэффициент при t^2
                case 3:
                    return (-x1 + 3 * x2 - 3 * x3 + x4) / 6.0f; //коэффициент при t^3
            }
 
            return 0;
        }
 
    }
}