Среда программирования:
Eclipse Mars.2(4.5.2)
Статья по теме:
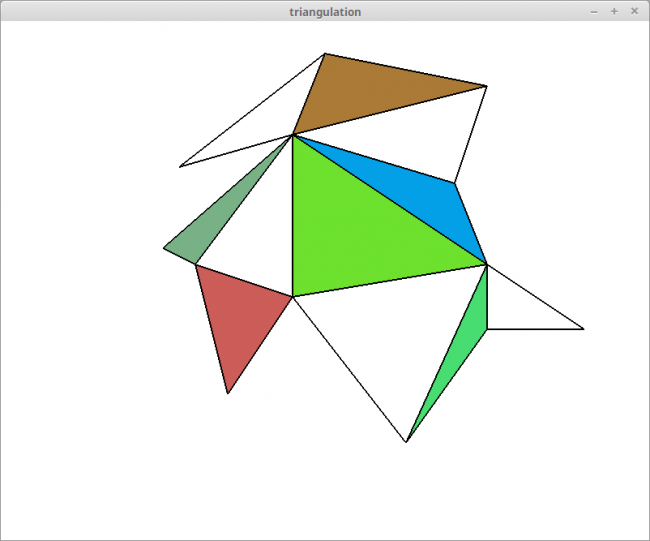
Задача: Используя алгоритм триангуляции разбить невыпуклый многоугольник на треугольники. Закрашивать треугольники, полученные при разбиении, через один. Первый закрашиваем, второй - нет и т.д.
Алгоритм триангуляции, рассматриваемый в данной статье, основывается на том, что n-угольник может быть разбит на n-2 треугольника путем проведения n-3 хорд. Для удобства реализации дополнительно были введены классы List(кольцевой двусвязный список) и Node(узел списка).
Код программы:
List.h
#ifndef LIST_H #define LIST_H #include <vector> using namespace std; class Node { //узел списка(в данной задаче-вершина многоугольника) public: double x, y; //координаты текущей точки Node *prev, *next; //указатели на предыдущую и следующую вершины //конструктор по умолчанию Node (double a = 0.0, double b = 0.0): x(a), y(b), prev(0), next(0) {} }; //направление, в котором заданы координаты(по часовой стрелке, против часовой стрелки) typedef enum { clockwise, count_clockwise, error } type; class List { //кольцевой двусвязный список(будет содержать координаты многоугольника) public: int size; //количество вершин Node* cur; //указатель на текущую вершину List (int s = 0, Node* tmp = 0): size(s), cur(tmp) {} bool is_empty () { return ( size == 0 ? true : false ); } void insert (double a, double b);//вставка одной вершины после текущей void insert (double *a, int n); //вставка массива координат Node* find (double a, double b); //поиск вершины с заданными координатами void delete_node (double a, double b); //удаление вершины с заданными координатами double cross_prod (Node *first, Node *second, Node *third);//векторное произведение type direction (); //направление обхода многоугольника //принадлежность остальных вершин многоугольника треугольнику с вершинами {first, second, third} bool is_in_triangle (Node *first, Node *second, Node *third); vector <List> triangulation (); //триангуляция }; #endif /* LIST_H*/
List.cpp
#include <vector> #include "List.h" using namespace std; void List :: insert (double a, double b) { Node *tmp = new Node; tmp->x = a; tmp->y = b; if ( is_empty() ) { tmp->next = tmp; tmp->prev = tmp; } else { tmp->next = cur->next; cur->next = tmp; tmp->prev = cur; tmp->next->prev = tmp; } cur = tmp; //меняем указатель на текущую вершину(вставленная вершина) size++; } void List :: insert (double *a, int n) { Node *tail = 0; /*добавлять массив из координат можно только в пустой список, иначе он будет замкнут неправильно*/ if ( is_empty() ) { for ( int i = 0; i < n; i += 2 ) { insert (a[i], a[i + 1]); //сохраняем указатель на начало списка, чтобы потом его замкнуть if ( i == 0 ) tail = cur; } //замыкаем список cur->next = tail; cur->next->prev = cur; cur = cur->next; } } Node* List :: find (double a, double b) { Node *tmp = cur; if ( !is_empty() ) { do { if ( a == tmp->x && b == tmp->y ) return tmp; else tmp = tmp->next; } while ( tmp != cur ); } return 0; } void List :: delete_node (double a, double b) { Node *tmp = find (a, b); if (tmp) { //вершина с такими координатами найдена //если удаляется текущая вершина, смещаем указатель на предыдущую if ( tmp == cur ) cur = cur->prev; tmp->prev->next = tmp->next; tmp->next->prev = tmp->prev; delete tmp; size--; } } //векторное произведение векторов, заданных точками {first, second} и {first, third} double List :: cross_prod (Node *first, Node *second, Node *third) { double x1 = second->x - first->x, x2 = third->x - first->x, y1 = second->y - first->y, y2 = third->y - first->y; return (x1 * y2 - x2 * y1); } type List :: direction () { Node *tmp = cur, *min = cur; double min_x = tmp->x, min_y = tmp->y; /*поиск самой левой точки(с минимальным значением абсциссы) если таких несколько, выберем нижнюю из них(с минимальным значением ординаты)*/ if ( !is_empty() ) { do { if ( tmp->x < min_x ) { min_x = tmp->x; min = tmp; } if ( tmp->x == min_x && tmp->y < min_y ) { min_y = tmp->y; min = tmp; } tmp = tmp->next; } while ( tmp != cur ); /*направление обхода зависит от знака векторного произведения между векторами, задаваемыми "минимальной" вершиной и двумя соседними с ней*/ return ( ( cross_prod ( min, min->next, min->prev ) < 0) ? clockwise : count_clockwise ); } return error; } bool List :: is_in_triangle ( Node *first, Node *second, Node *third ) { double a, b, c; Node *tmp = cur; do { if ( tmp != first && tmp != second && tmp != third ) { a = cross_prod(tmp, first, second); b = cross_prod(tmp, second, third); c = cross_prod(tmp, third, first); //какая-либо из точек многоугольника попадает внутрь треугольника if ( ( a > 0 && b > 0 && c > 0 ) || ( a < 0 && b < 0 && c < 0 ) ) return true; } tmp = tmp->next; } while ( tmp != cur ); return false; } vector <List> List :: triangulation () { //массив, c координатами треугольников, образующими триангуляцию vector <List> triangles, empty(0, 0); //empty будет возвращен в случае ошибки List *l; //список координат треугольника //берем три последовательно расположенные вершины Node *first = cur, *second = cur->next, *third = cur->next->next; //определяем направление обхода(по часовой стрелке/против часовой стрелки) type cond = direction(); double prod; if ( cond != error ) { while (size > 3) { prod = cross_prod(first, second, third); /*вторая вершина должна лежать левее прямой, соединяющей first и third, если вершины заданы по часовой стрелке и правее прямой, если против часовой стрелки*/ if ( ( cond == clockwise && prod < 0 ) || ( cond == count_clockwise && prod > 0 ) ) { //внутри треугольника нет других вершин многоугольника if ( !is_in_triangle ( first, second, third ) ) { l = new List; l->insert(first->x, first->y); l->insert(second->x, second->y); l->insert(third->x, third->y); triangles.push_back(*l); //исключаем вершину second из рассмотрения delete_node(second->x, second->y); delete l; } second = third; third = third->next; } else { first = second; second = third; third = third->next; } } if (size == 3) { //добавляем последний треугольник l = new List; l->insert(first->x, first->y); l->insert(second->x, second->y); l->insert(third->x, third->y); triangles.push_back(*l); delete l; } return triangles; } return empty; }
main.cpp
#include <cstdlib> #include <ctime> #include <vector> #include "List.h" #include <GL/glut.h> #define width 800 #define height 640 using namespace std; //координаты многоугольника(заданы по часовой стрелке) double coords[] = { 140.0, 90.0, 120.0, 170.0, 100.0, 180.0, 180.0, 250.0, 110.0, 230.0,200.0, 300.0, 300.0, 280.0, 280.0, 220.0, 300.0, 170.0, 360.0, 130.0, 300.0, 130.0, 250.0, 60.0, 180.0, 150.0}; int size = sizeof(coords) / sizeof(coords[0]); void init () { glClearColor (1.0, 1.0, 1.0, 1.0); //цвет фона(RGBA, белый) glViewport (0, 0, width, height); //область вывода glMatrixMode (GL_PROJECTION); //матрица преобразований(матрица проекций) glLoadIdentity (); //замена текущей матрицы на единичную /*матрица двухмерной ортографической проекции, параметры функции определяют левую, правую, нижнюю и верхнюю плоскости отсечения*/ gluOrtho2D (0, width / 2, 0, height / 2); } void draw_polygon () { /*1-й параметр-число координат вершины, 2-й-тип данных, 3-й-смещение от координат одной вершины до координат следующей,4-й-указатель на массив с координатами*/ glVertexPointer(2, GL_DOUBLE, 0, coords); glEnableClientState (GL_VERTEX_ARRAY); //тип массива(массив вершин) //вывод примитивов типа замкнутая ломанная glDrawArrays(GL_LINE_LOOP, 0, size / 2); glFlush (); //вывод на экран } void draw_triangle (double x1, double y1, double x2, double y2, double x3, double y3) { glColor3ub (0, 0, 0); glBegin(GL_LINE_LOOP); //тип примитива(замкнутая ломанная) //координаты вершин glVertex2d (x1, y1); glVertex2d (x2, y2); glVertex2d (x3, y3); glEnd(); glFlush(); } void fill_triangle (double x1, double y1, double x2, double y2, double x3, double y3) { glColor3ub (rand () % 254, rand() % 254, rand() % 254); glBegin(GL_TRIANGLES); glVertex2d (x1, y1); glVertex2d (x2, y2); glVertex2d (x3, y3); glEnd(); glFlush(); } void triangulate () { draw_polygon(); List *polygon; polygon = new List; polygon->insert (coords, size); //инициализация многоугольника //применение триангуляции vector <List> triangles = polygon->triangulation(); double x1, y1, x2, y2, x3, y3; srand (time(0)); int i = 1; //номер треугольника for (auto now : triangles) { x1 = now.cur->x, y1 = now.cur->y, x2 = now.cur->next->x, y2 = now.cur->next->y, x3 = now.cur->prev->x, y3 = now.cur->prev->y; if ( i % 2 ) //закрашиваем треугольники с нечётными номерами fill_triangle(x1, y1, x2, y2, x3, y3); //прорисовываем границы draw_triangle(x1, y1, x2, y2, x3, y3); i++; } delete polygon; } void display () { glClear (GL_COLOR_BUFFER_BIT); //очистка текущего буфера цвета glColor3ub (0, 0, 0); //установка цвета рисования(RGB, черный) glLineWidth (2); //ширина линии в пикселях //построение и триангуляция многоугольника с координатами из массива coords triangulate(); } int main ( int argc, char** argv ) { glutInit(&argc, argv); glutInitDisplayMode(GLUT_SINGLE | GLUT_RGB); //режим окна(одиночный буфер и RGB-палитра) glutInitWindowSize (width, height); //установка размеров окна(ширина и высота в пикселях) glutInitWindowPosition (200, 30);//положение окна относительно левого верхнего угла экрана glutCreateWindow ("triangulation");//создание окна c указанным заголовком glutDisplayFunc(display); //вывод на экран init (); //дополнительные параметры glutMainLoop(); return 0; }
| Прикрепленный файл | Размер |
|---|---|
| kolesnikova_triangulation_of_polygon.zip | 132.5 кб |





Комментарии
Чет не работает, помогите, надо очень сильно