Среда программирования:
Code::Blocks 16.01
Статья по теме:
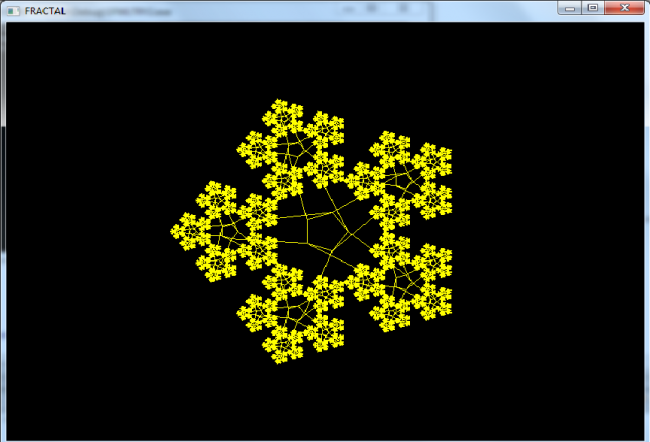
Программа создающая фрактал "Зевзда Дюрера".
Код программы:
#include <SFML\Graphics.hpp> #include <SFML\Window.hpp> #include <iostream> #include <math.h> using namespace std; const int winW = 750; //ширина const int winH = 550; //высота const float magicPi = 3.141596 / 5; //в статье константа //Построение фрактала void setFractal(float x, float y, float r, float angle, int deep, sf::VertexArray & target_va) { double h = 2 * r * cos(magicPi); //расстояние от центра пятиугольника до каждого центра внешних пятиугольников for (int i = 0; i < 5; i++) { float ang2 = angle + magicPi*i * 2, x2 = x - h*cos(ang2), y2 = y - h*sin(ang2), rad2 = r / (2 * cos(magicPi) + 1), ang3 = angle + 3.141596 + (2 * i + 1)*magicPi; for (int j = 0; j < 4; j++) { sf::Vertex tmp_x, tmp_y; tmp_y.color = tmp_x.color = sf::Color::Yellow; //Задаем цвет временным переменным. tmp_x.position = sf::Vector2f((x + rad2*cos(ang3 + j*magicPi * 2)), (y + rad2*sin(ang3 + j*magicPi * 2))); //Вычисляем позицию верш х tmp_y.position = sf::Vector2f((x + rad2*cos(ang3 + (j + 1)*magicPi * 2)), (y + rad2*sin(ang3 + (j + 1)*magicPi * 2))); target_va.append(tmp_x); target_va.append(tmp_y); } //Условие выхода if (deep > 0) setFractal(x2, y2, r / (2 * cos(magicPi) + 1), angle + 3.141596 + (2 * i + 1)*magicPi, deep - 1, target_va); } } int main() { sf::RenderWindow window(sf::VideoMode(winW, winH), "FRACTAL"); //Окно программы sf::VertexArray va; //наш массив вершин va.setPrimitiveType(sf::Lines); //рисуем линией setFractal(winW/2, winH/2, 70, 0, 7, va); //Вызов функции прорисовки while (1) { sf::Event event; while (window.pollEvent(event)) { //Ждет событие // События закрытия окну по клику на крестик и по нажатию Esc if (event.type == sf::Event::Closed || event.type == sf::Event::KeyPressed && event.key.code == sf::Keyboard::Escape) return 0; } window.clear(); window.draw(va); window.display(); } return 0; }
| Прикрепленный файл | Размер |
|---|---|
| Zvezda durera.zip | 774.34 кб |




