Среда программирования:
Lazarus 0.9.30 win 32
Статья по теме:
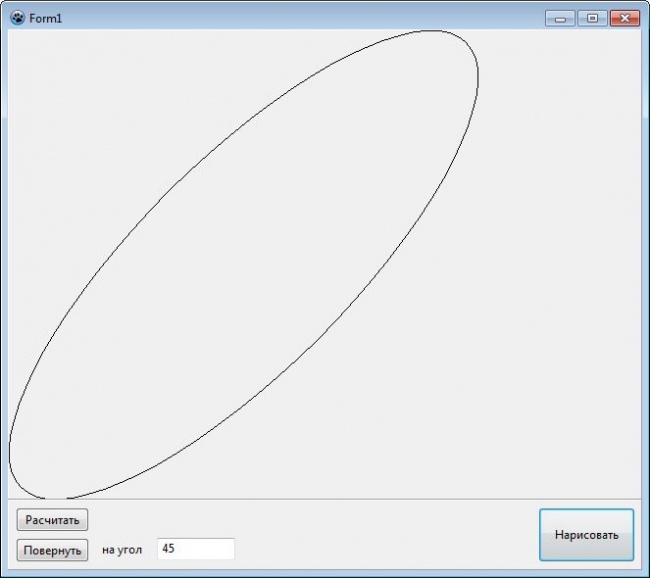
Программа, демонстрирующая поворот эллипса на произвольный угол и его отрисовку в экранной области. Точки фигуры рассчитываются в мировых координатах и заносятся в массив. Любые преобразования производятся с мировыми координатами. После чего, по нажатию кнопки "Нарисовать", производится поиск коэффициентов масштабирования и пересчет мировых координат в экранные.
Код программы:
unit Unit1; {$mode objfpc}{$H+} interface uses Classes, SysUtils, FileUtil, Forms, Controls, Graphics, Dialogs, StdCtrls, ExtCtrls; type { TForm1 } TForm1 = class(TForm) Button1: TButton; Button2: TButton; Button3: TButton; Edit1: TEdit; Label1: TLabel; PaintBox1: TPaintBox; Panel1: TPanel; Panel2: TPanel; procedure Button1Click(Sender: TObject); procedure Button2Click(Sender: TObject); procedure Button3Click(Sender: TObject); private { private declarations } public { public declarations } end; var Form1: TForm1; x, y: array [1..500] of double; // Массив точек фигуры count : Integer; implementation {$R *.lfm} { TForm1 } procedure TForm1.Button1Click(Sender: TObject); Var i : Integer; a : Double; begin // Занесение всех точек фигуры в массив a := 0; i := 0; While a <= 2*Pi do begin i := i+1; x[i] := 3*cos(a); // Параметрическое уравнение эллипса y[i] := sin(a); a := a+Pi/36; end; // Количество точек фигуры сохраняем в переменной count count := i; ShowMessage('Построение закончено'); end; procedure TForm1.Button2Click(Sender: TObject); Var a, bx : Double; i : Integer; begin // Поворот фигуры a := pi*StrToInt(Edit1.Text)/180; // Угол поворота for i := 1 to count do begin bx := x[i]; x[i] := x[i]*cos(a) - y[i]*sin(a); y[i] := bx*sin(a) + y[i]*cos(a); end; ShowMessage('Поворот произведен'); end; procedure TForm1.Button3Click(Sender: TObject); Var Xmin,Xmax,Ymin,Ymax : Double; SXmax,SXmin,SYMax,SYmin : Integer; Scalex, Scaley, Scale : Double; sx,sy : Integer; i : Integer; begin Xmin:=x[1]; Ymin:=y[1]; Xmax:=x[1]; Ymax:=y[1]; // Поиск размеров прямоугольника, в котором находится фигура for i := 1 to count do begin if x[i] < Xmin then Xmin:=x[i]; if x[i] > Xmax then Xmax:=x[i]; if y[i] < Ymin then Ymin:=y[i]; if y[i] > Ymax then Ymax:=y[i]; end; // Размеры экранной области SXmin:=0; SXmax:=PaintBox1.Width; SYmin:=0; SYmax:=PaintBox1.Height; // Поиск коэффициентов масштабирования ScaleX:=(SXmax - SXmin)/(Xmax - Xmin); ScaleY:=(SYmax - SYmin)/(Ymax - Ymin); // Однородное масштабирование if ScaleX < ScaleY then Scale:= ScaleX else Scale:= ScaleY; // Пересчет в экранные координаты for i:=1 to count do begin sx:=SXmin+round(Scale*(x[i] - Xmin)); sy:=SYmax-round(Scale*(y[i] - Ymin)); if i = 1 then PaintBox1.Canvas.MoveTo(sx,sy) else PaintBox1.Canvas.LineTo(sx,sy); end; end; end.
| Прикрепленный файл | Размер |
|---|---|
| Исходные коды и исполняемый файл | 765.29 кб |




