С помощью этого алгоритма можно закрашивать любые замкнутые области. Исходными данными для этого алгоритма являются цвет границы области и точка, принадлежащая этой области (т.н. затравочный пиксел). Суть метода заключается в следующем: мы берём затравочную точку и закрашиваем её. Для каждого незакрашенного соседа мы выполняем аналогичную процедуру. Т.о. мы получаем рекурсивный алгоритм, описание которого на псевдокоде представлено ниже:
1. Поместить затравочный пиксел в стек;
2. Извлечь пиксел из стека;
3. Присвоить пикселу требуемое значение (цвет внутренней области);
4. Каждый окрестный пиксел добавить в стек, если он
4.1. Не является граничным;
4.2. Не обработан ранее (т.е. его цвет отличается от цвета границы или цвета внутренней области);
5. Если стек не пуст, перейти к шагу 2.
Разумеется, можно использовать как четырёх-, так и восьмисвязную окрестность.
Недостатков у этого алгоритма больше, чем преимуществ: он медленный и расходует много памяти для стека, поэтому гораздо правильнее будет перейти к рассмотрению следующей группы алгоритмов.
Этот алгоритм подходит только для тех случаев, когда закрашиваемая область может быть задана в виде многоугольника. Будем считать, что мы работаем с многоугольником с вершинами P1,P2,…,PN и требуется отобразить его на экране вместе со всеми внутренними точками. Для удобства будем предполагать, что каждое ребро многоугольника задаётся координатами его концов x1,y1 и x2,y2 (при этом y2≥y1). Также условимся, что координата x возрастает при движении слева направо, а координата y при движении сверху вниз.
Подавляющее большинство алгоритмов растеризации многоугольников основаны на следующем предположении: любая секущая прямая пересекает границу многоугольника чётное число раз. Это утверждение неверно только в двух случаях:
- Когда секущая прямая содержит ребро;
- Когда секущая прямая содержит вершину, а смежные рёбра лежат по одну сторону от секущей прямой.
Эти два случая довольно легко обнаружить, поэтому при рассмотрении алгоритмов растеризации многоугольников будем считать, что приведённое выше предположение всегда верно.
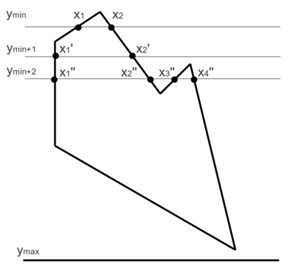
Алгоритм, основанный на работе со списком рёберных точек, состоит из трёх основных этапов:
На первом этапе растеризуются все негоризонтальные рёбра многоугольника. Для каждого значения y составляется список x-координат, закрашенных при растеризации. Например, для рассматриваемого многоугольника мы получим следующие значения (при движении по часовой стрелке):
На втором этапе для каждого значения y списки упорядочиваются по возрастанию. После этого списки будут выглядеть следующим образом:
На третьем этапе для каждого y заполняются все полученные отрезки.
Преимущество этого алгоритма в том, что каждый пиксель обрабатывается строго один раз. Т.о. можно утверждать, что этот алгоритм подходит для устройств, где доступ к видео-памяти занимает сравнительно много времени.
Существует модификация данного алгоритма, оптимизированная по расходу памяти. В ней на каждом шаге обрабатываются только те рёбра, которые пересекаются с текущей линией развёртки.
Этот метод растеризации многоугольников основан на свойствах логической операции исключающего ИЛИ (XOR).
Этот алгоритм, как и алгоритм со списком рёберных точек, начинается с растеризации границ. После того, как границы построены, закрашивание сводится к заполнению в каждой строке промежутков между двумя закрашенными точками.
Представим изображение в виде бинарного массива I. Договоримся, что I[x;y]=1, когда пиксел закрашен, и I[x;y]=0, когда пиксел не закрашен. Легко заметить, что применение операции I[x+1,y]=I[x;y]XOR I[x+1;y] ко всем пикселам в строке приведёт к почти идеальному результату. В результате этой операции будут закрашены все промежутки, но последний пиксел в каждом промежутке не будет закрашен. В большинстве случаев эта погрешность несущественна и незаметна, но если требуется получить точный результат, можно после завершения алгоритма повторно вывести на экран границы, или воспользоваться небольшой модификацией этого алгоритма.
for y:=1 to YMax do
begin
fl:=false;
for x:=1 to XMax do
begin
if I[x,y]=1 then
fl:=not fl;
if fl then
I[x,y]:=1;
end;
end;Преимущество этого алгоритма в его предельной простоте и высокой скорости. Недостаток в том, что алгоритм не может работать, при наличии посторонних изображений.
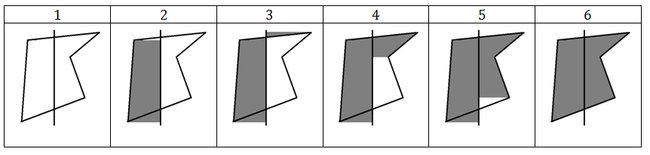
Алгоритм XOR для гранейМетод XOR для граней описывается следующим простым алгоритмом: Для каждого ребра в многоугольнике инвертируются цвета всех пикселов, расположенных правее этого ребра. При этом порядок обхода рёбер не имеет значения. В таблице приведены шаги этого алгоритма (движение по часовой стрелке):
Недостаток этого алгоритма – высокие временные затраты, так как некоторые пикселы обрабатываются более одного раза. Кроме того, чем больше расстояние от изображения до правой границы области экрана, тем больше будет совершено лишних операций.
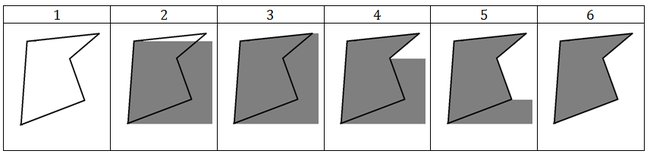
От некоторых из недостатков свободен модифицированный вариант алгоритма XOR для граней. Он называется алгоритм XOR для граней с перегородкой. Его идея заключается в том, чтобы инвертировать область не между ребром и границей экрана, а между ребром и специальной вертикальной линий (т.н. перегородкой). Чаще всего перегородка проводится так, чтобы она пересекала многоугольник. Шаги работы алгоритма приведены в таблице.