Среда программирования:
Embarcadero Delphi XE ver. 15
Статья по теме:
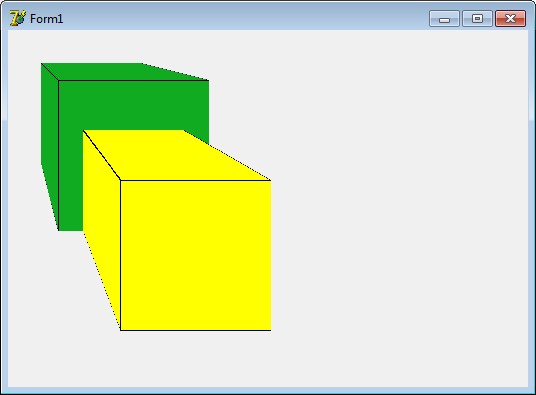
В программе используется алгоритм удаления невидимых граней - алгоритм z-буфера. Рисуем два тела, одно тело частично закрывает другое. В конкретном примере это куб позади куба.
Для построения сцены необходимо щелкнуть на форме левой кнопкой мыши. Невидимые грани куба перекрываются видимыми, в результате получаем визуально объемную картинку.
Код программы:
unit Unit1; interface uses Windows, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms, Dialogs, Math, ExtCtrls; type TForm1 = class(TForm) pb1: TPaintBox; procedure Cube(a: Array of Integer); procedure DrawVerge(x1, x2, y1, y2, z1, z2: Integer); procedure pb1Click(Sender: TObject); private { Private declarations } public { Public declarations } end; var Form1: TForm1; buf: Array [0..800] of Array [0..600] of Integer; i, j, k, xe, ye, xe2, ye2, r, g, b: Integer; koef: Double; implementation {$R *.dfm} procedure TForm1.Cube(a: array of Integer); // прорисовка куба по входным данным begin DrawVerge(Min(a[0], a[1]), Max(a[0], a[1]), Min(a[2], a[3]), Max(a[2], a[3]), a[4], a[4]); DrawVerge(a[0], a[0], Min(a[2], a[3]), Max(a[2], a[3]), Min(a[4], a[5]), Max(a[4], a[5])); DrawVerge(Min(a[0], a[1]), Max(a[0], a[1]), Min(a[2], a[3]), Max(a[2], a[3]), a[5], a[5]); DrawVerge(a[1], a[1], Min(a[2], a[3]), Max(a[2], a[3]), Min(a[4], a[5]), Max(a[4], a[5])); DrawVerge(Min(a[0], a[1]), Max(a[0], a[1]), a[2], a[2], Min(a[4], a[5]), Max(a[4], a[5])); DrawVerge(Min(a[0], a[1]), Max(a[0], a[1]), a[3], a[3], Min(a[4], a[5]), Max(a[4], a[5])); end; // просчет координат сторон куба procedure TForm1.DrawVerge(x1, x2, y1, y2, z1, z2: Integer); begin with pb1.Canvas do begin for i := x1 to x2 do begin // цикл прорисовки пикселей от x1 до x2 for j := y1 to y2 do begin // цикл прорисовки пикселей от y1 до y2 for k := z1 to z2 do begin // цикл прорисовки пикселей от z1 до z2 // расчет координат пикселей xe := Round((koef * i) / (k + koef)); ye := Round((koef * j) / (k + koef)); if(buf[xe][ye] > k) then begin buf[xe][ye] := k; //проверка границ куба if((i = x1) or (i = x2)) and ((j = y1) or (j = y2)) or ((i = x1) or (i = x2)) and ((k = z1) or (k = z2)) or ((j = y1) or (j = y2)) and ((k = z1) or (k = z2))then Pixels[xe, ye] := clBlack // цвет ребер куба else Pixels[xe, ye] := RGB(r, g, b); // Цвет пикселя end; end; end; end; end; end; procedure TForm1.pb1Click(Sender: TObject); begin with pb1.Canvas do begin for i := 0 to 800 do begin for j := 0 to 600 do begin buf[i][j] := 1234567890; end; end; koef := 300; r := 16; g := 171; b := 32; Cube([100, 400, 100, 400, 300, 600]); r := 255; g := 255; b := 0; Cube([150, 350, 200, 400, 100, 300]); end; end; end.
| Прикрепленный файл | Размер |
|---|---|
| Демонстрационный проект алгоритма Z-буфера | 378.1 кб |




