Интерполяционный многочлен Эрмита

Общая информация
Интерполирование по Эрмиту есть специальный вид многоинтервальной интерполяции, при котором интерполирующий многочлен H_n(х) обеспечивает не только равенство H_n(х) значениям f(x), но и совпадение некоторого количества производных в узлах интерполяции.
Многочлен Эрмита единственный, это следует из однозначности его построения.
Остаточный член интерполяционной формулы Эрмита равен:
R_n(x)=f(x)-H_n(x)=f⁽ⁿ⁺¹⁾(ξ)*(x-x₀)^N₀*...*(x-x_m)^N_m/(n+1)!, где ξ∈[x₀,x_m]
Алгоритм построения

Представим себе, что на плоскости в координатах x,y нарисовано несколько точек. Задача соединить их плавной кривой так чтобы в итоге получился график гладкой функции y=ƒ(x).
На каждом отдельном участке между соседними точками это должен быть многочлен третьей степени и при этом соседние многочлены должны каким-то образом гладко
сопрягаться.
Для того, чтобы решить эту задачу, сначала решим частную задачу: представим себе что на отрезке [0;1] у нас задана функция - многочлен третьей степени:ƒ(x)=а₀+a₁*x+a₂*x²+a₃*x³
Нам неизвестны коэффициенты a₀,a₁,a₂,a₃ и мы хотим определить их по следующим данным:ƒ(0)=y₀,ƒ(1)=y₁,ƒ' (0)=z₀,ƒ'(1)=z₁
Производная функции ƒ определяется следующим образом:ƒ'(x)=a₁+2*a₂*x+3*a₃*x²
Запишем наши уравнения:f(0)=a₀=y₀f'(0)=a₁=z₀f(1)=a₀+a₁+a₂+a₃=y₁
f'(1)=a₁+2*a₂+3*a₃=z₁
Было бы удобно записать эти уравнения в матричном виде:

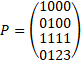
Правая часть системы линейных уравнений, это столбец с координатами y₀,z₀,y₁,z₁

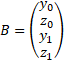
Вектор-столбец неизвестных переменных обозначим

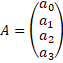
Тогда нам нужно решить систему линейных уравнений P*A=B

В общем случае решением будет: A=P^-1*B

Воспользуемся алгоритмом Гаусса:
для этого в левой части таблицы запишем матрицу P, a справа приписывается единичная матрица

Задача привести матрицу некоторыми преобразованиями к такому виду, чтобы слева оказалась единичная матрица, а то что будет в правой половине и будет обратной матрицей

(P│E)→ (E│P^-1)

Итак,

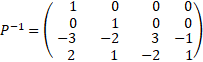
По значениям в концах отрезка [0,1] и их производных, мы восстановили всю функцию

a₀=y₀
a₁=z₀
a₂=-3*y₀-2*z₀+3*y₁-z₁
a₃=2*y₀+z₀-2*y₁+z₁
ƒ(x)=y₀+z₀*x+(-3*y₀-2*z₀+3*y₁-z₁)*x²+(2*y₀+z₀-2*y₁+z₁)*x³

Пусть нужно произвести интерполяцию на отрезке [x₀;x₁ ], тогда график функции необходимо сдвинуть на x₀ и растянуть в x₁-x₀ раз, а поскольку z₀,z₁ в x₁-x₀ раз меньше, чем требуется, то их необходимо домножить.
Для удобства введем k=(x-x₀)/(x₁-x₀) и h=x₁-x₀. Функция примет вид:

ƒ(k)=y₀+z₀*h*k+(-3*y₀-2*z₀*h+3*y₁-z₁*h)*k²+(2*y₀+z₀*h-2*y₁+z₁*h)*k³

Аналогичным образом определяется многочлен любой степени.
При добавлении значений производных (до некоторого порядка m) в точках добавляются дополнительные слагаемые.
Точность растет с увеличением количества известных значений производных в точках.