Вычислительная геометрия

Данный алгоритм позволяет строить эллипсы на сновании координат центра фигуры и длин большей и меньшей полуосей.
Алгоритм является модификацией алгоритма для генерации окружностей.

С помощью данного алгоритма можно заполнить (зарисовать) любую окружность.

Теоретическое обоснование метода заключаются в использовании свойства квадрата и теоремы Пито: " в выпуклый четырёхугольник ABCD можно вписать окружность тогда и только тогда, когда суммы его противоположных сторон равны ".

Ориентированная площадь треугольника – это обычная площадь, снабженная знаком. Знак ориентированной площади треугольника АВС такой же, как у ориентированного угла между векторами AB и AC. То есть ее знак зависит от порядка перечисления вершин.

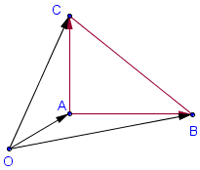
Рисунок №1

Суть алгоритма поиска в ширину в том, что мы обходим связный граф таким образом, что сначала мы рассматриваем родителя, потом по очереди рассматриваем его предков, потом рассматриваем предков его предков и т.д.
Порядок обхода вершин графа.

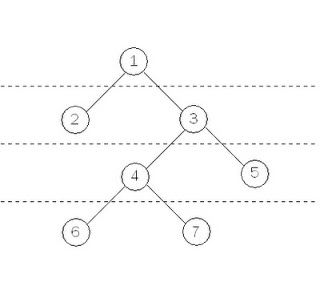
Можно объяснить алгоритм двумя способами:

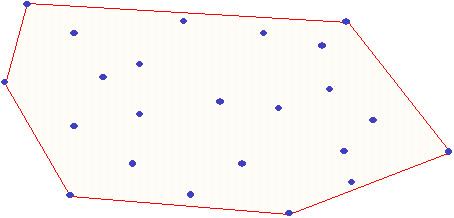
Пусть на плоскости задано некоторое количество точек. Оболочкой множества данных точек называется любая замкнутая линия, которая содержит в себе все эти точки.
Соответственно минимальная выпуклая оболочка - это такая оболочка, которая является выпуклым многоугольником наименьшего периметра.

Это один из простейших алгоритмов удаления невидимых поверхностей. Впервые он был предложен Кэтмулом. Работает этот алгоритм в пространстве изображения.

Предположим, что нам необходимо определить принадлежность точки а полигону р. Для этого из некоторой удаленной точки проведем прямую линию в точку а. На этом пути может встретиться нуль или несколько пересечений границы полигона: при первом пересечении мы входим внутрь полигона, при втором — выходим из него, при третьем пересечении снова входим внутрь и так до тех пор, пока не достигнем точки а. Таким образом каждое нечетное пересечение означает попадание внутрь полигона р, а каждое четное — выход из него.

С помощью этого алгоритма можно закрашивать любые замкнутые области. Исходными данными для этого алгоритма являются цвет границы области и точка, принадлежащая этой области (т.н. затравочный пиксел). Суть метода заключается в следующем: мы берём затравочную точку и закрашиваем её. Для каждого незакрашенного соседа мы выполняем аналогичную процедуру. Т.о. мы получаем рекурсивный алгоритм, описание которого на псевдокоде представлено ниже:

1. Поместить затравочный пиксел в стек;
2. Извлечь пиксел из стека;

Алгоритм Ву — это алгоритм разложения отрезка в растр со сглаживанием. Был предложен У Сяолинем (Xiaolin Wu, отсюда устоявшееся в русском языке название алгоритма) в статье, опубликованной журналом Computer Graphics в июле 1991 года. Алгоритм сочетает высококачественное устранение ступенчатости и скорость, близкую к скорости алгоритма Брезенхема без сглаживания.

См. исправленный алгоритм Брезенхема построения окружности здесь https://cgraph.ru/node/308

Во многих областях приложений, таких как, например, системы автоматизированного проектирования машиностроительного направления, естественными графическими примитивами, кроме отрезков прямых и строк текстов, являются и конические сечения, т.е. окружности, эллипсы, параболы и гиперболы. Наиболее употребительным примитивом, естественно, является окружность. Один из наиболее простых и эффективных алгоритмов генерации окружности разработан Брезенхемом.