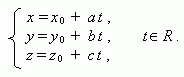Графика в пространстве (3D)

В решении задачи удаления невидимых линий и поверхностей можно выделить два основных подхода:
Первый подход заключается в определении для каждого пикселя того объекта, который вдоль направления проектирования является ближайшим к нему. При этом работа ведется в пространстве картинной плоскости и существенно используются растровые свойства дисплея.

Сам алгоритм плавающего горизонта может иметь несколько различных реализаций. Его основная идея - это выстроить границу на экране, заходя за которые, точка не будет отрисовываться. В данной статье алгоритм работает следующим образом:

1. Алгоритм берёт точку графика и пытается разместить её на экране
2. Алгоритм отрисовывает точку графика, если хотя бы одно условие ниже выполняется:
   • Точка выше всех пикселей в столбце экрана
   • Точка ниже всех пикселей в столбце экрана
   • Точка левее всех пикселей в строке экрана

Матрицей поворота (или матрицей направляющих косинусов) называется ортогональная матрица, которая используется для выполнения собственного ортогонального преобразования в евклидовом пространстве. При умножении любого вектора на матрицу поворота длина вектора сохраняется. Определитель матрицы поворота равен единице.

Кватернионы были придуманы Роуэном Уильямом Гамильтоном как альтернатива матричным вращениям. Вращение при помощи кватернионов сводится к умножению чисел, что очень просто в программной реализации.

Алгоритм:
Входные данные:
1) угол θ на который производится вращение.
2) координаты x, y, z вращаемой точки.
3) координаты i, j, k направляющего единичного вектора, вокруг которого происходит вращение.

Рассмотрим ортогональные проекции, используемые в техническом черчении, в регламентированной для него правосторонней системе координат, когда ось Z изображается вертикальной. Затем будут проиллюстрированы аксонометрические проекции также в правосторонней системе координат, но уже более близкой к машинной графике (ось Y вертикальна, ось X направлена горизонтально вправо, а ось Z - от экрана к наблюдателю).

Пример построения центральной проекции куба смотрите на странице https://cgraph.ru/node/221

Для того, чтобы увидеть на плоскости монитора трехмерное изображение, нужно уметь задать способ отображения трехмерных точек в двумерные. В общем случае проекции преобразуют точки, заданные в системе координат размерностью n в точки системы координат размерностью меньшей, чем n. В нашем случае точки трехмерного пространства преобразуются в точки двумерного пространства.

Уравнение прямой, проходящей через две различные точки
( х₁, у₁, z₁ ) и ( х₂, у₂ , z₂ ):

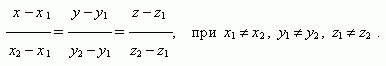
Параметрическое уравнение прямой, проходящей через точку ( х₀ , у₀ , z₀ ) и параллельной направляющему вектору прямой ( a, b, с ) :