Среда программирования:
Lazarus
Статья по теме:
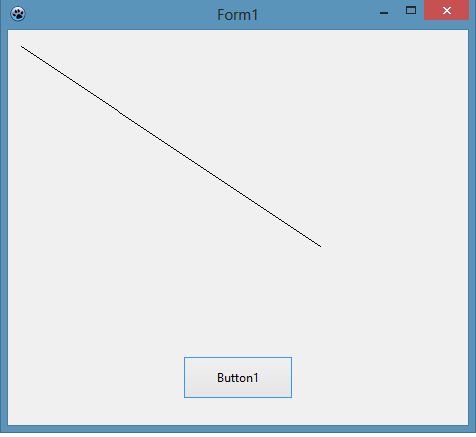
Провести прямую линию между двумя точками, заданными своими координатами. Использовать растровый алгоритм Брезенхэма.
Алгоритм основан на том, что для каждой точки растра существует ровно 4 соседних точки. Это означает, что две соседние точки могут отличаться друг от друга только по одной координате и только на 1 единицу. Т. е. для точки (x, y) соседними являются точки (x+1, y), (x-1, y), (x, y+1), (x, y-1). Точка (x+1, y+1) может оказаться закрашенной только если закрашена точка (x+1, y) или (x, y+1). Алгоритм Брезенхема модифицированный по такому закону реализован в данной программе.
Код программы:
unit Unit1; {$mode objfpc}{$H+} interface uses Classes, SysUtils, FileUtil, Forms, Controls, Graphics, Dialogs, ExtCtrls, StdCtrls; type { TForm1 } TForm1 = class(TForm) Button1: TButton; PaintBox1: TPaintBox; procedure Button1Click(Sender: TObject); private { private declarations } public { public declarations } end; var Form1: TForm1; implementation {$R *.lfm} { TForm1 } procedure DrawLine(x0,y0,x1,y1:integer;col:TColor); var dx,dy,sx,sy,d,d1,d2,x,y,i:integer; begin if (x1>x0) then dx:=x1-x0 else dx:=x0-x1; if (y1>y0) then dy:=y1-y0 else dy:=y0-y1; if (x1>=x0) then sx:=1 else sx:=-1; if (y1>=y0) then sy:=1 else sy:=-1; if (dy<dx) then begin d:=(dy<<1)-dx; d1:=dy<<1; d2:=(dy-dx)<<1; Form1.PaintBox1.Canvas.Pixels[x0,y0]:=col; x:=x0+sx; y:=y0; for i:=1 to dx do begin if (d>0) then begin d:=d+d2; y:=y+sy; end else d:=d+d1; Form1.PaintBox1.Canvas.Pixels[x,y]:=col; x:=x+sx; end; end else begin d:=(dx<<1)-dy; d1:=dx<<1; d2:=(dx-dy)<< 1; Form1.PaintBox1.Canvas.Pixels[x0,y0]:=col; x:=x0; y:=y0+sy; for i:=1 to dy do begin if (d>0) then begin d:=d+d2; x:=x+sx; end else d:=d+d1; Form1.PaintBox1.Canvas.Pixels[x,y]:=col; y:=y+sy; end; end; end; procedure TForm1.Button1Click(Sender: TObject); begin DrawLine(0,0,300,200,clBlack); end; end.
| Прикрепленный файл | Размер |
|---|---|
| Исходные коды | 254.88 кб |
| Запускаемый файл | 2.43 Мб |




