Среда программирования:
Lazarus
Статья по теме:
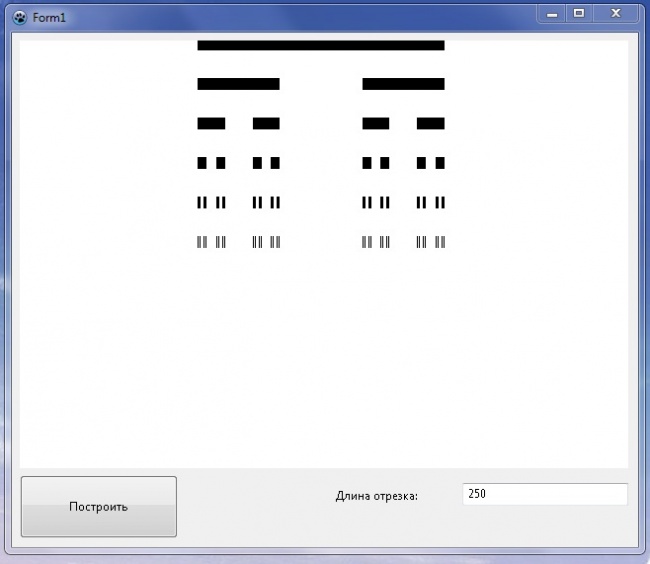
Программа демонстрирует построение Канторового множества.
Для начала работы нужно ввести длину отрезка в соответствующее поле и нажать кнопку "Построить". При желании можно ввести новую длину и заново построить множество.
Код программы:
unit Unit1; {$mode objfpc}{$H+} interface uses Classes, SysUtils, FileUtil, Forms, Controls, Graphics, Dialogs, StdCtrls, ExtCtrls, Buttons; type { TForm1 } TForm1 = class(TForm) BitBtn1: TBitBtn; Edit1: TEdit; Label1: TLabel; PaintBox1: TPaintBox; procedure BitBtn1Click(Sender: TObject); private { private declarations } public { public declarations } procedure Draw_Kanter(x, y, Otrw:Double); end; var Form1: TForm1; implementation {$R *.lfm} { TForm1 } //Отработка кнопки построения procedure TForm1.BitBtn1Click(Sender: TObject); Var Otr, x : Double; begin //Очистка окна PaintBox PaintBox1.Canvas.Brush.Color := clWhite; PaintBox1.Canvas.FillRect(Canvas.ClipRect); //Считывание введенной длины отрезка Otr := StrToInt(Edit1.Text); //Расчет координаты по Х x := 610/2 - Otr/2; //Вызов функции отрисовки мн-ва Кантера Draw_Kanter(x,10,Otr); end; procedure TForm1.Draw_Kanter(x, y, Otrw :Double); begin //Цвет кисти - черный PaintBox1.Canvas.Brush.Color := clBlack; //Выполнимо, пока отрезки не будут меньше 1 if Otrw >= 1 then begin //Рисуем отрезок в виде прямоугольника, для наглядности PaintBox1.Canvas.Rectangle(round(x), round(y), round(x+Otrw), round(y-12)); //Сдвигаемся вниз y := y + 40; //Рисуем следующие отрезки мн-ва, дроблением отрезка на 3 части Draw_Kanter(x + Otrw*2/3, y, Otrw/3); Draw_Kanter(x, y, Otrw/3); end; end; end.
| Прикрепленный файл | Размер |
|---|---|
| Kanter.rar | 692.33 кб |





Комментарии
Спасибо за статью. Я не Ваш студент. Но мне она помогла написать функцию для Канторова множества на Python для черепашки:
import turtle
def kanter(x, y, d):
if d > 1:
turtle.penup() # Поднять хвост
turtle.goto(x, y) # Иди в точку
turtle.pendown() # Опусти хвост
turtle.forward(d) # Иди вперед (рисуем новую линию)
y -= 20 # Идем ниже для следующей линии
# Рисуем следующие отрезки мн-ва, дроблением отрезка на 3 части:
kanter(x, y, d / 3)
kanter(x + d * 2 / 3, y, d / 3)
turtle.shape('turtle') # Отображаемая фигура при рисовании
turtle.pensize(3) # Толщина линии
i = 567 # Длина линии нулевой итерации
kanter(-300, 200, i) # Запуск рекурсии (итерации отрезков длиной до 1)
turtle.done()