Интерполяция полиномом Ньютона

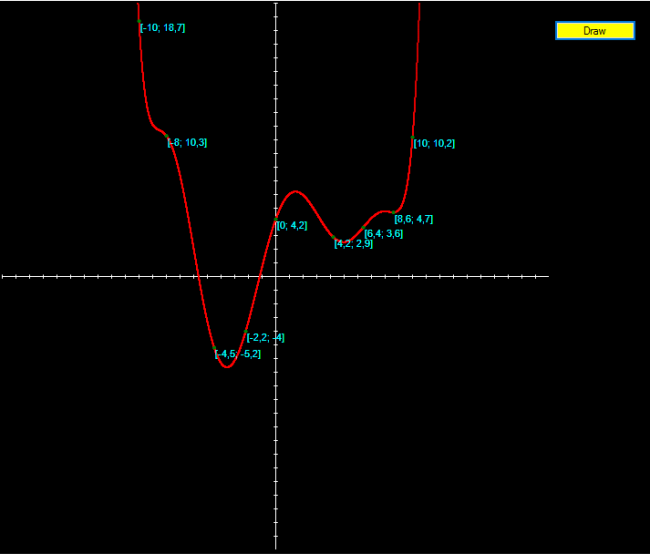
using System;
using System.Collections.Generic;
using System.ComponentModel;
using System.Data;
using System.Drawing;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
using System.Windows.Forms;
 
namespace Newton_Interpolate
{
    public partial class Form1 : Form
    {
 
        public struct point //Структура точки
        {
            public double X, Y; //Машинные координаты
            public double x, y; //Реальные координаты
        }
 
 
        //Координаты исходных точек.
        public double[,] Pts = { { -10, 18.7 }, 
                                 { -8, 10.3 }, 
                                 { -4.5, -5.2 }, 
                                 { -2.2, -4 },
                                 { 0, 4.2},
                                 {4.2, 2.9},
                                 {6.4, 3.6},
                                 {8.6, 4.7},
                                 {10, 10.2}
                               };
 
        public point[] Points = new point[100]; //Массив точек
        public Font drawFont = new Font("Arial", 8); //Стиль шрифта и его размер, для отрисовки координат точек на плоскости
        public int xc=300, yc=300; //Координаты центра координатных осей
 
 
        public Form1()
        {
            InitializeComponent();
        }
 
        //Отрисовка плоскости, с точками и координатными осями
        public void drawPlain()
        {
            Graphics g = Graphics.FromHwnd(picturebox1.Handle); 
            g.SmoothingMode = System.Drawing.Drawing2D.SmoothingMode.AntiAlias;
 
            g.Clear(Color.Black);
            Pen Axis = new Pen(Color.White, 1);
 
            g.DrawLine(Axis, 0, 300, 600, 300);
            g.DrawLine(Axis, 300, 0, 300, 600);
 
            for (int i = 0; i <= 600; i += 15)
            {
                g.DrawLine(Axis, i, 298, i, 302);
                g.DrawLine(Axis, 298, i, 302, i);
            }
 
            for (int i = 0; i < (Pts.Length / 2); i++)
            {
                Points[i].x = Pts[i, 0];
                Points[i].y = Pts[i, 1];
                Points[i].X = xc + Points[i].x * 15;
                Points[i].Y = yc - Points[i].y * 15;
            }
 
            DrawPoints();//Отрисовка точек
        }
 
        public int ChangeCoordinates(double a, int isY) //Перевод координат из реальных в машинные
        {
            if (isY == 1) return (int)(yc - a * 15);
            return (int)(xc + a * 15);
        }
 
 
        //Высчитывание полинома Ньютона в заданном отрезка, с заданными точками.
        public double Newton(double x)
        {
            double res = Points[0].y, F = 0, den = 1, n = Pts.Length/2;
            int i, j, k;
            for (i = 1; i < n; i++)
            {
                F = 0;
                for (j = 0; j <= i; j++)
                {
                    den = 1;
                    for (k = 0; k <= i; k++)
                    {
                        if (k != j) den *= (Points[j].x - Points[k].x);
                    }
                    F += Points[j].y / den;
                }
                for (k = 0; k < i; k++) F *= (x - Points[k].x);
                res += F;
            }
            return res;
        }
 
 
        //Отрисовка точек и их координат на плоскости
        public void DrawPoints()
        {
            Graphics g = Graphics.FromHwnd(picturebox1.Handle);
            g.SmoothingMode = System.Drawing.Drawing2D.SmoothingMode.AntiAlias;
 
            SolidBrush pointBrush = new SolidBrush(Color.Green);
            SolidBrush drawPointBrush = new SolidBrush(Color.Cyan);
 
            for (int i = 0; i < (Pts.Length / 2); i++)
            {
                g.FillEllipse(pointBrush, (float)Points[i].X - 2, (float)Points[i].Y - 2, 4, 4);
                String drawString = "[" + Points[i].x + "; " + Points[i].y + "]";
                PointF drawPoint = new PointF((float)Points[i].X, (float)Points[i].Y);
                g.DrawString(drawString, drawFont, drawPointBrush, drawPoint);
            }
        }
 
 
        //Отрисовка интерполированной функции по нажатию на кнопку "Draw"
        private void Draw_Button_Click(object sender, EventArgs e)
        {
            Graphics g = Graphics.FromHwnd(picturebox1.Handle);
            g.SmoothingMode = System.Drawing.Drawing2D.SmoothingMode.AntiAlias;
 
            SolidBrush drawLineNewton = new SolidBrush(Color.Red);
 
            drawPlain();
 
            for (double i = -15.0f; i <= 15.0f; i += 0.0005f)
            {
                g.FillEllipse(drawLineNewton, ChangeCoordinates(i, 0), ChangeCoordinates(Newton(i), 1), 1, 1);
            }
            DrawPoints();
 
        }
    }
}