
Замощение (паркет) — разбиение плоскости на многоугольники (мозаику) без наложений и зазоров с повторяющимся узором.
Виды паркетов
Правильные паркеты
Паркеты, составленные из симметричных многоугольников, называются правильными. В евклидовом пространстве замощение возможно лишь с помощью треугольников, четырёхугольников и шестиугольников, так как общий угол каждой из этих фигур способен делить и 180°, и 360°.
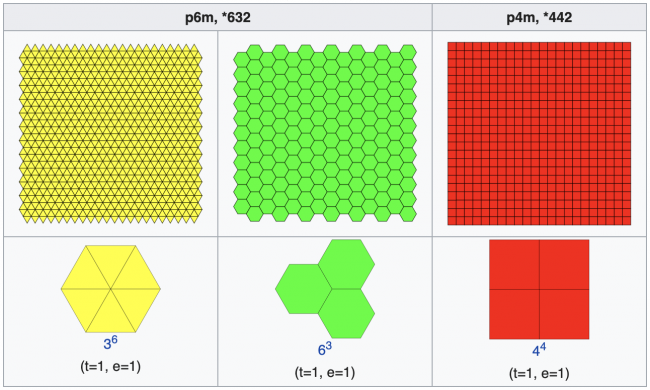
Правильные паркеты
Полуправильные паркеты
Паркеты, состоящие из правильных многоугольников двух или более типов, такие, что для любых двух вершин паркета существует преобразование симметрии (самосовмещение), переводящее одну из них в другую, называются полуправильными. Их также называют архимедовыми или равномерыми.
В случае полуправильных паркетов замощение из одинаковых правильных многоугольников в евклидовом пространстве невозможно, поскольку общий угол одного такого многоугольника не будет делить ни 180°, ни 360°.
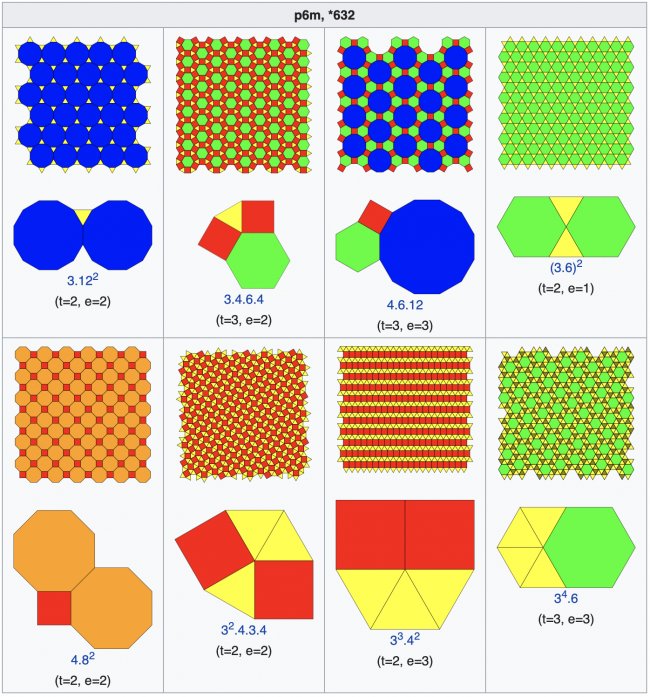
Полуправильные паркеты
Периодические паркеты
Паркет с повторяющимся шаблоном, совмещающимся при сдвиге в различных направлениях, называется периодическим.

Периодический паркет
Непериодический паркет
Паркет, в котором отсутсвует повторяющийся шаблон, называется непериодическим.

Непериодический паркет
Квазиправильный паркет
Полуправильный паркет, который имеет в точности два вида правильных граней, поочерёдно следующие вокруг каждой вершины, называется квазиправильным.

Квазиправильный паркет




