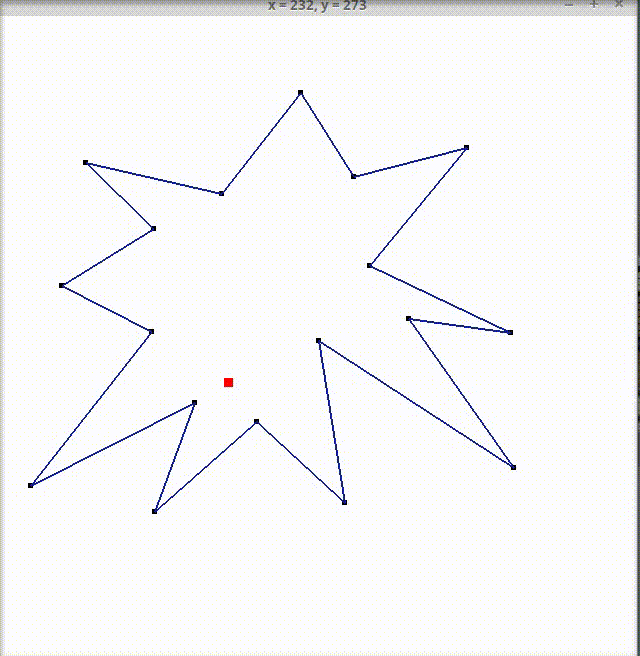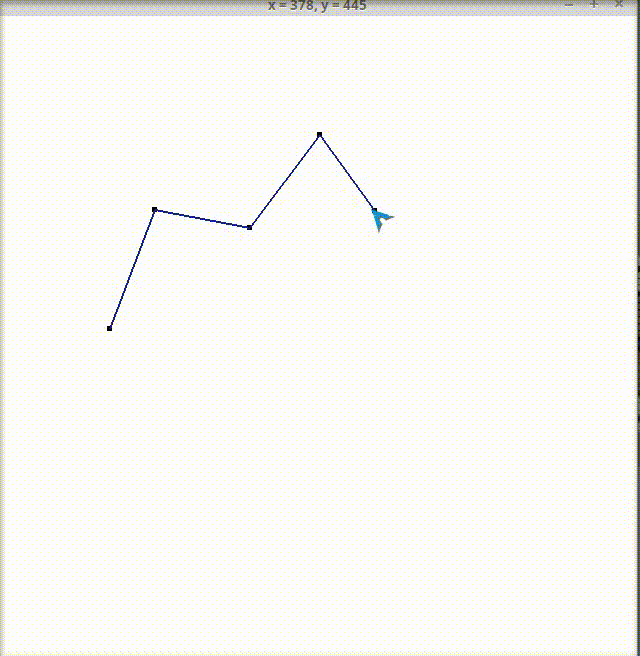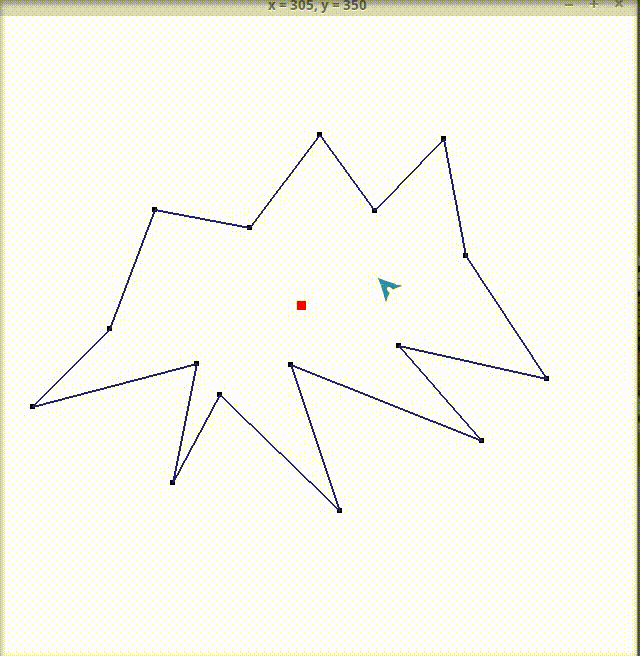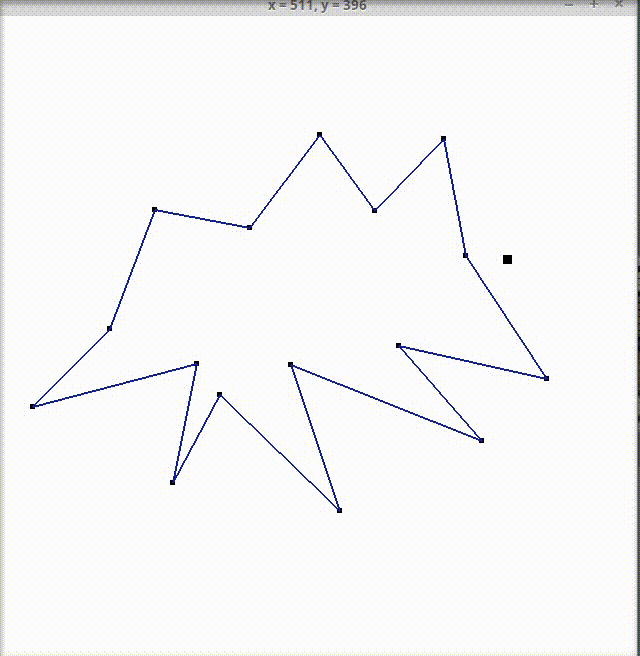
Задача: определить, принадлежит ли точка многоугольнику.
Для запуска приложения на Linux достаточно открыть файл is_in_polygon(см. архив во вложении), предварительно сделав его исполняемым(chmod +x либо Свойства-Права-Разрешить исполнять как программу). После запуска появится белое окно, в заголовке которого отображаются координаты последнего нажатия левой кнопки мыши(начальные значения x = 0, y = 0). По щелчку левой кнопки мыши в произвольном месте окна на месте нажатия рисуется точка и проводится линия из предыдущей точки в новую(если указаны хотя бы 2 точки), таким образом можно построить любой многоугольник. При нажатии клавиши Enter завершается построение многоугольника(многоугольник нельзя будет больше изменить), последняя точка соединяется с первой.
Далее по щелчку левой кнопки мыши на месте нажатия рисуется точка и закрашивается красным цветом, если она лежит внутри или на границе многоугольника, черным- если вне многоугольника. При следующем нажатии предыдущие проверяемые точки не прорисовываются, проверять можно сколько угодно точек, пока не надоест :)
При нажатии правой кнопки мыши происходит очистка окна и сброс всех ранее введенных координат, можно заново рисовать многоугольник и проверять, какие точки ему принадлежат. Для выхода из приложения можно нажать крестик в правом верхнем углу окна либо клавишу Esc.
Для проверки принадлежности точки многоугольнику используется горизонтальный луч, направленный вправо, с началом в проверяемой точке. В качестве вспомогательной на луче взята точка, абсцисса которой совпадает с шириной окна.
points.h
#ifndef POINTS_H #define POINTS_H #include <vector> using namespace std; struct Vertex { //вершина int x, y; //координаты вершины //конструктор по умолчанию Vertex ( int a = 0, int b = 0 ) : x(a), y(b) {} }; //положение точки(внутри, снаружи, на границе) typedef enum { in, out, border } point_position; //векторное произведение double cross_prod ( Vertex, Vertex, Vertex ); //скалярное произведение double scalar_prod ( Vertex, Vertex, Vertex ); //лежит ли точка на ребре bool is_point_on_edge ( Vertex, Vertex, Vertex ); //пересекается ли ребро с лучом bool is_edge_cross ( Vertex, Vertex, Vertex, Vertex ); //выбор точки на луче Vertex point_on_ray ( Vertex, int ); //расположение точки относительно многоугольника(внутри/снаружи/на границе) point_position is_point_in_polygon ( vector <Vertex>, Vertex, int ); #endif /* POINTS_H*/
points.cpp
#include "points.h" #include <vector> using namespace std; //[ {ab} x {ac} ] double cross_prod ( Vertex a, Vertex b, Vertex c ) { double x1 = b.x - a.x, y1 = b.y - a.y, x2 = c.x - a.x, y2 = c.y - a.y; return ( x1 * y2 - x2 * y1 ); } //( {ab}, {ac} ) double scalar_prod ( Vertex a, Vertex b, Vertex c ) { double x1 = b.x - a.x, y1 = b.y - a.y, x2 = c.x - a.x, y2 = c.y - a.y; return ( x1 * x2 + y1 * y2 ); } //точка c лежит на ребре ab, если она лежит на одной прямой с ab(векторное произведение = 0), //и c лежит между a и b(скалярное произведение <= 0; = 0, когда c совпадает с a или c b) bool is_point_on_edge ( Vertex a, Vertex b, Vertex c ) { double prod1 = cross_prod ( a, b, c ), prod2 = scalar_prod ( c, a, b ); return ( prod1 == 0 && prod2 <= 0 ) ? true : false; } //пересекаются ли отрезки ab и cd bool is_edge_cross ( Vertex a, Vertex b, Vertex c, Vertex d ) { double prod1, prod2, prod3, prod4; prod1 = cross_prod ( a, b, c ); prod2 = cross_prod ( a, b, d ); prod3 = cross_prod ( d, c, a ); prod4 = cross_prod ( d, c, b ); //отрезки ab и cd пересекаются, если c и d лежат по разные стороны от ab, //a и b лежат по разные стороны от cd bool is_cross = (prod1 * prod2 < 0 && prod3 * prod4 < 0); //надо проверить, не принадлежат ли концы одного отрезка другому //в этом случае одно(или несколько) векторных произведений обратятся в ноль bool cond1, cond2, cond3, cond4, cond1_1, cond2_1, cond3_1, cond4_1, is_one_inside_other; cond1 = is_point_on_edge ( a, b, c ); cond2 = is_point_on_edge ( a, b, d ); cond3 = is_point_on_edge ( c, d, a ); cond4 = is_point_on_edge ( c, d, b ); //проверка, что только один конец одного из отрезков принадлежит другому //таким образом, из рассмотрения исключаюся ребра, лежащие на луче cond1_1 = ( cond1 && ! ( cond2 || cond3 || cond4 ) ); cond2_1 = ( cond2 && ! ( cond1 || cond3 || cond4 ) ); cond3_1 = ( cond3 && ! ( cond1 || cond2 || cond4 ) ); cond4_1 = ( cond4 && ! ( cond1 || cond2 || cond3 ) ); is_one_inside_other = ( cond1_1 || cond2_1 || cond3_1 || cond4_1 ); return ( is_cross || is_one_inside_other) ? true : false; } //выбор точки на луче, проходящем через проверяемую точку point; в качестве такой точки //выбрана крайняя точка окна, лежащая на одной горизонтальной прямой с point Vertex point_on_ray ( Vertex point, int scr_width ) { Vertex ray ( scr_width, point.y ); return ray; } //положение точки относительно многоугольника point_position is_point_in_polygon ( vector <Vertex> polygon, Vertex begin, int scr_width ) { Vertex first, second; //вершины многоугольника //получение второй точки, лежащей на луче Vertex end = point_on_ray ( begin, scr_width ); unsigned count = 0; //кол-во пересечений с лучом if ( polygon.empty() ) return out; //не было передано ни одной вершины if ( polygon.size() == 1 ) //была передана одна вершина return ( ( polygon[0].x == begin.x && polygon[0].y == begin.y ) ? border : out ); if ( polygon.size() == 2 ) { //был передан отрезок second.x = polygon[1].x; second.y = polygon[1].y; first.x = polygon[0].x; first.y = polygon[0].y; return ( is_point_on_edge ( first, second, begin ) ? border : out ); } //был передан по крайней мере треугольник for ( unsigned i = 1; i <= polygon.size(); i++ ) { if ( i < polygon.size() ) { second.x = polygon[i].x; second.y = polygon[i].y; first.x = polygon[i - 1].x; first.y = polygon[i - 1].y; } else { //обрабатываем последнее ребро(последняя и первая вершины) second.x = polygon[0].x; second.y = polygon[0].y; first.x = polygon.back().x; first.y = polygon.back().y; } //принадлежит ли точка ребру if ( is_point_on_edge ( first, second, begin ) ) return border; //точка на границе //пересекается ли ребро с лучом(при этом исключаются ребра, лежащие на луче) if ( is_edge_cross ( first, second, begin, end ) ) //определяем нижнюю вершину по y //ребро не лежит на одной прямой с горизонтальным лучом (из предыдущего условия) //если выбрать не горизонтальный луч, надо дополнительно рассмотреть горизонтальные ребра if ( ( first.y > second.y && second.y < begin.y ) || ( first.y < second.y && first.y < begin.y ) ) count++; //нижний конец ребра ниже луча } if ( count % 2 ) return in; //нечетное кол-во пересечений с горизонтальным лучом return out; }
main.cpp
#include <cstdio> #include <cstdlib> #include <vector> #include "points.h" #include <GL/glut.h> #define width 800 #define height 640 #define ESC 27 //десятичный код клавиши Esc #define ENTER 13 //десятичный код клавиши Enter using namespace std; int mouse_x = 0, mouse_y = 0; //координаты точки при последнем нажатии левой кнопки мыши bool enter_flag = false; //была ли нажата клавиша Enter vector <Vertex> polygon, points; //здесь будут сохраняться координаты Vertex *ptr; //вспомогательный указатель void draw_dot () { if ( !points.empty() ) { //прорисовка вершин многоугольника glPointSize ( 5 ); //размер точки в пикселях (5х5 пикселей) glBegin ( GL_POINTS ); //тип примитива(точка) glColor3ub ( 0, 0, 0 ); //установка цвета рисования(RGB, черный) //прорисовываем точками все вершины for ( auto now : points ) glVertex2i ( now.x, now.y ); glEnd (); //была нажата клавиша Enter, построение многоугольника завершено if ( enter_flag ) { Vertex point; //точка, проверяемая на принадлежность многоугольнику glPointSize ( 9 ); //проверяем квадрат 9x9, т.к. размер точки 9х9 пикселей //координаты точки содержатся в mouse_x, mouse_y for ( int i = mouse_x - 4; i <= mouse_x + 4; i++ ) { for ( int j = mouse_y - 4; j <= mouse_y + 4; j++ ) { point.x = i; point.y = j; if ( is_point_in_polygon ( polygon, point, width ) == in || is_point_in_polygon( polygon, point, width ) == border ) { //если точка внутри или на границе, меняем цвет рисования на красный glColor3ub ( 255, 0, 0 ); i = mouse_x + 5; //для выхода из внешнего цикла break; } } } glBegin ( GL_POINTS ); //рисуем точку на месте последнего щелчка мыши glVertex2i ( mouse_x, mouse_y ); glEnd (); } } } void draw_line () { if ( !polygon.empty() ) { glColor3ub ( 18, 31, 154 ); //синий glLineWidth ( 2 ); //толщина линии glBegin ( GL_LINES ); //тип примитива-линия //соединяем по две соседние вершины for ( unsigned i = 1; i < polygon.size(); i++ ) { glVertex2i ( polygon[ i - 1].x, polygon[i - 1].y ); glVertex2i ( polygon[i].x, polygon[i].y ); } if ( enter_flag ) { //построение завершено, соединяем первую и последнюю вершины glVertex2i ( polygon[0].x, polygon[0].y ); glVertex2i ( polygon.back().x, polygon.back().y ); } glEnd (); } } void reshape ( int w, int h ) { glViewport ( 0, 0, width, height ); //область вывода glLoadIdentity (); //замена текущей матрицы на единичную gluOrtho2D ( 0, width, 0, height ); //плоскость отсечения glMatrixMode ( GL_MODELVIEW ); //матрица преобразований glFlush(); } //создание заголовка окна с координатами точки void generate_window_title () { char *str; str = new char [50]; //выделение памяти под строку //формирование заголовка sprintf ( str, "x = %d, y = %d", mouse_x, mouse_y ); glutSetWindowTitle ( str ); //установка заголовка delete [] str; } void display () { generate_window_title(); //обновление заголовка glClear (GL_COLOR_BUFFER_BIT); //очистка текущего буфера цвета draw_dot (); //прорисовка вершин и точки draw_line(); //прорисовка ребер glFlush(); //вывод на экран } void mouse ( int button, int state, int x, int y ) { if ( state == GLUT_DOWN ) //нажата кнопка switch ( button ) { //если левая кнопка case GLUT_LEFT_BUTTON: mouse_x = x; mouse_y = height - y; //запоминаем новые координаты точки if ( !enter_flag ) { //добавляем новые координаты(если не был нажат Enter) ptr = new Vertex ( mouse_x, mouse_y ); polygon.push_back(*ptr); points.push_back(*ptr); delete ptr; } break; //если правая кнопка case GLUT_RIGHT_BUTTON: //сбрасываем координаты mouse_x = 0; mouse_y = 0; //освобождаем память polygon.clear(); points.clear(); //сбрасываем флаг Enter enter_flag = false; break; } glutPostRedisplay (); //обратный вызов функции перерисовки окна } void keyboard ( unsigned char key, int x, int y ) { switch ( key ) { case ESC: //если был нажат esc, выходим из приложения exit (ESC); break; case ENTER: //если enter enter_flag = true; //устанавливаем флаг glutPostRedisplay (); //вызываем функцию перерисовки для отображения последнего ребра break; } } int main ( int argc, char** argv ) { glutInit( &argc, argv ); //инициализация OpenGL Utility Toolkit glutInitDisplayMode( GLUT_SINGLE | GLUT_RGB ); //режим окна(одиночный буфер и RGB-палитра) glutInitWindowSize ( width, height ); //установка размеров окна(ширина и высота в пикселях) glutInitWindowPosition ( 200, 30 );//положение окна относительно левого верхнего угла экрана glutCreateWindow ( "" ); //создание окна glutReshapeFunc ( reshape ); //перерисовка окна при измении его размеров или положения glutDisplayFunc ( display );//инициализация функции, отвечающей за рисование в окне glutMouseFunc ( mouse ); //обработка мыши glutKeyboardFunc ( keyboard ); //обработка клавиатуры glClearColor ( 1.0, 1.0, 1.0, 1.0 ); //цвет фона(RGBA, белый) glutMainLoop (); //вход в главный цикл return 0; }
| Прикрепленный файл | Размер |
|---|---|
| kolesnikova_ray_tracing_for_polygon.zip | 141.3 кб |




