Среда программирования:
Lazarus
Статья по теме:
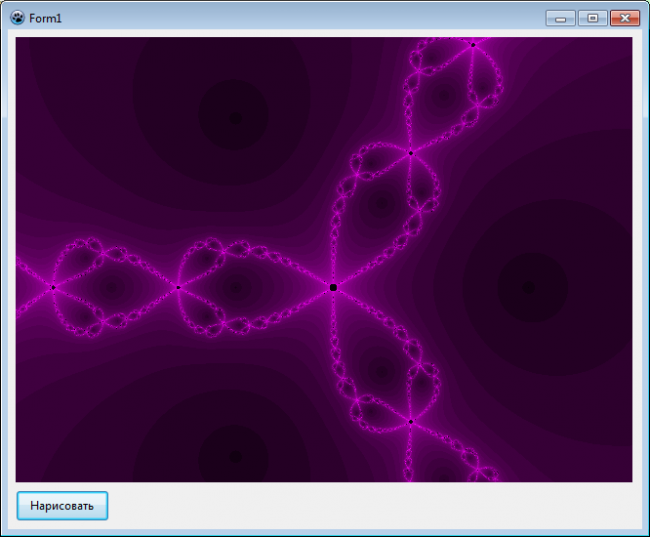
Бассейны Ньютона, фракталы Ньютона — разновидность алгебраических фракталов.
Области с фрактальными границами появляются при приближенном нахождении корней нелинейного уравнения алгоритмом Ньютона на комплексной плоскости (для функции действительной переменной метод Ньютона часто называют методом касательных, который, в данном случае, обобщается для комплексной плоскости).
Код программы:
unit Unit1; {$mode objfpc}{$H+} interface uses Classes, SysUtils, FileUtil, Forms, Controls, Graphics, Dialogs, StdCtrls, ExtCtrls; type { TForm1 } TForm1 = class(TForm) Button1: TButton; PaintBox1: TPaintBox; procedure Button1Click(Sender: TObject); private { private declarations } public { public declarations } end; var Form1: TForm1; implementation {$R *.lfm} { TForm1 } procedure TForm1.Button1Click(Sender: TObject); type Complex = Record x : Real; y : Real; end; const iter = 50; max = 1e+6; min = 1e-6; var z, t, d : Complex; p : Real; x, y, n : Integer; Cancel : Boolean; gd, gm : Smallint; mx, my : Integer; col: TColor; begin Randomize; PaintBox1.Canvas.Clear; Mx := PaintBox1.Canvas.Width div 2; My := PaintBox1.Canvas.Height div 2; for y := -my to my do for x := -mx to mx do begin n := 0; z.x := X * 0.005; z.y := Y * 0.005; d := z; while (sqr(z.x)+sqr(z.y) < max) and (sqr(d.x)+sqr(d.y) > min) and (n < iter) do begin t := z; {z^3 - 1} p := sqr(sqr(t.x)+sqr(t.y)); z.x := 2/3*t.x + (sqr(t.x)-sqr(t.y))/(3*p); z.y := 2/3*t.y*(1-t.x/p);{} d.x := abs(t.x - z.x); d.y := abs(t.y - z.y); Inc(n); end; col := (n*9) mod 255; PaintBox1.Canvas.Pixels[mx+x,my+y]:=RGBTOColor(col,0,col); end; end; end.
| Прикрепленный файл | Размер |
|---|---|
| Исходные коды и исполняемый файл | 763.67 кб |




