Среда программирования:
Brackets build 1.14.2-17770
Статья по теме:
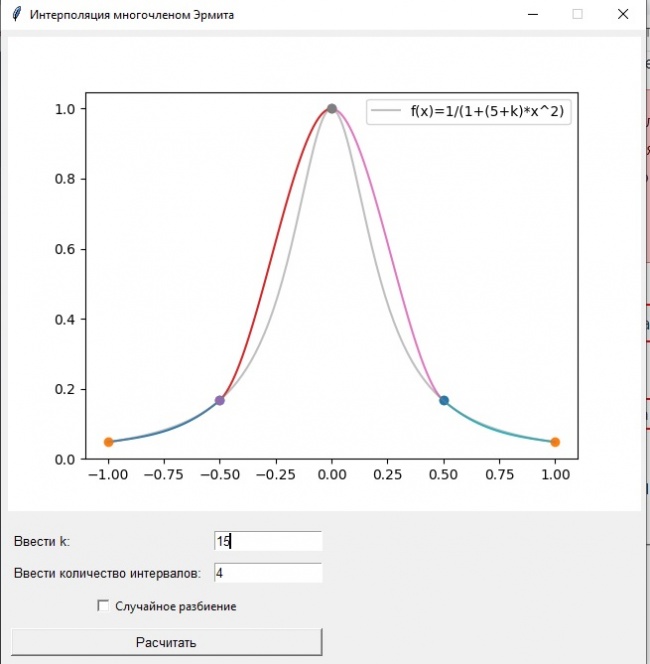
Программа демонстрирующая интерполяцию многочленом Эрмита третьей степени
функции ƒ(x)=1/(1+(5+k)*x2)
Код программы:
from tkinter import * from tkinter import messagebox from PIL import ImageTk, Image import numpy as np import matplotlib.pyplot as plt import random class Application(Frame): def __init__(self,master=None): super().__init__(master) self.grid() self.create_widgets() self.master.title("Интерполяция многочленом Эрмита") self.master.geometry(f"650x640+50+50") self.master.resizable(False, False) def create_widgets(self): left_frame = Frame(root, width=640, height=480, pady=5).grid(row=0,sticky="wens") right_frame = Frame(root,width=640, height=160, padx=5, pady=5) right_frame.grid(row=1,sticky="wens") # холст для вывода графика функции и ее апроксимации self.canvas = Canvas(left_frame,width=640,height=480) self.canvas.grid(row=0, column=0,sticky="wens", pady=5, padx=5) # ввод коэффициента k для функции Label(right_frame,text="Ввести k:",font=('Arial',10)).grid( row=0, column=0,sticky="w", pady=5, padx=5) self.parD = DoubleVar() Entry(right_frame,textvariable = self.parD,width=15,font=('Arial',10)).grid( row=0,column=1,sticky="w",padx=5,pady=5) # ввод количества интервалов разбиения Label(right_frame,text="Ввести количество интервалов:",font=('Arial',10)).grid( row=1, column=0,sticky="w", pady=5, padx=5) self.NumberOfIntervals = IntVar() Entry(right_frame,textvariable = self.NumberOfIntervals,width=15,font=('Arial',10)).grid( row=1,column=1,sticky="w",padx=5,pady=5) # если переменная CheckVar = 0 равномерная сетка, случайные абсциссы иначе self.CheckVar= IntVar() R1 = Checkbutton(right_frame, text = "Случайное разбиение", variable = self.CheckVar, onvalue = 1, offvalue = 0).grid(row=2,column=0,sticky="we",padx=5,pady=5,columnspan=2) # кнопка для вывода графика Button(right_frame,text="Расчитать",font=('Arial',10),command=lambda: self.calc()).grid( row=3,column=0,columnspan=2, stick="we",padx=5,pady=5) # метод для вычисления интерполяционного многочлена эрмита на передаваемом отрезке def ermite(self,Ax,Ay,Bx,By,prA,prB): xe=np.arange(Ax,Bx+0.01,0.01) h=Bx-Ax fxde=[] for xde in xe: koef=(xde-Ax)/h h3=(1-3*(koef**2)+2*(koef**3))*Ay+(3*(koef**2)-2*(koef**3))*By+(koef-2*(koef**2)+(koef**3))*prA*h+(-(koef**2)+(koef**3))*prB*h fxde.append(h3) # возвращаем два списка с координатами точек по эрмиту return xe,fxde def calc(self): # получаем коээф. k k=self.parD.get() # получаем разбиения n=self.NumberOfIntervals.get() # проверка, что интервал не нулевой if n == 0: messagebox.showwarning(title="Неверное значение", message="Введите количество интервалов больше 0") return xi=[] # равномерная сетка, если не выбранно обратное if self.CheckVar.get() == 0: for i in range(0,n+1): xi.append(-1+i*(2/n)) else: for i in range(0,n+1): xi.append(random.uniform(-1,1)) # поскольку точки случайные, для корректного счета сортируем xi.sort() fxi=[] prxi=[] # вычисляем значение функции и производной в точках разбиения for xd in xi: fxi.append(1/(1+(5+k)*(xd**2))) prxi.append(-(2*(k+5)*xd)/((k+5)*(xd**2)+1)**2) # попарно передаем точки, производные в точках и значения функции в метод вычисляющий многочлен эрмита # полученные два списка наносим на график for i in range(len(xi)-1): x,y=self.ermite(xi[i],fxi[i],xi[i+1],fxi[i+1],prxi[i],prxi[i+1]) plt.plot(x,y) plt.plot(xi[i],fxi[i],'o') plt.plot(xi[i+1],fxi[i+1],'o') # на отрезке [-1,1] находим абсциссы и ординаты для отображения иходного графика функции xfunc=np.arange(-1,1+0.01,0.01) yfunc=(1/(1+(5+k)*(xfunc**2))) plt.plot(xfunc,yfunc, color="gray",alpha=0.5,label='f(x)=1/(1+(5+k)*x^2)') plt.legend() # сохраняем картинку с графиками plt.savefig("ermite.png") # вызываем функцию загрузки картинки image = self.load_image("ermite.png") # выводим на холст картинку self.set_image(image) # очищаем все что было на графике plt.clf() # метод загрузки изображения def load_image(self,name): img = Image.open(name) return ImageTk.PhotoImage(img) # метод установки изображения на холст def set_image(self,image): self.canvas.delete("all") self.canvas.image = image self.canvas.create_image(0,0,image= self.canvas.image,anchor='nw') root = Tk() app = Application(master=root) root.mainloop()
| Прикрепленный файл | Размер |
|---|---|
| tsybrik_example_ermite.rar | 2.13 кб |




