Если посмотреть на многие вещи в природе, вы заметите, что они являются фрактальными. Они имеют различные уровни детализации. Типичным примером является очертание горного хребта. Оно содержит значительные различия в высоте (горы), средние изменения (холмы), небольшие вариации (валуны), крошечные изменения (камни) и так далее. Посмотрите на что угодно: распространение пятен травы на поле, волн в море, движение муравьев, движение ветвей дерева, узоры из мрамора, ветра. Все эти явления поддаются той же схеме, в больших и малых вариациях. Функция шума Перлина воссоздает это, просто складывая функции шума в различных масштабах.

Пример 2-мерного шума Перлина
Главная идея шума Перлина
Шум Перлина чаще всего реализуется как 2-х, 3-х или 4-х мерное пространство, но может быть реализован для n-мерного. Весь алгоритм состоит из 3 частей:
1. Заполнить сетку псевдослучайными векторами
2. Вычислить значение функции в каждой точке
3. Интерполирование между этими точками.
Заполнение сетки
Создадим n-мерную сеть. В каждом узле этой сетки создадим вектор из этого пространства (для 1-мерного пространства это число 1 или -1, для 2-мерного — случайный вектор для окружности и так далее для больших измерений)
Вычисление псевдослучайного градиента (помним что это из математического анализа?):
для 1 и 2-мерного пространства используем генератор случайных чисел. Для больших измерений используем Монте Карло.
Для уменьшения затрат процессорного времени и времени на вычисления можно использовать таблицу значений векторов, постоянно изменяя вектор умножением (сложением, делением и т. д.) на случайную константу.
Для двухмерного варианта требуется всего 4 — по количеству граней (у квадрата их 4). Вектора направлены (условно из центра куба/квадрата) в сторону каждой из граней и не нормализованы.
В двумерном случае каждому узлу сетки поставлен в соответствие один из 4 векторов:
{0;-1},{0;1},{-1;0},{1;0}. В зависимости от псевдослучайного числа, генерирующего эту сетку мы и получаем один из этих векторов. Эти вектора указывают направление изменения интерполяции.
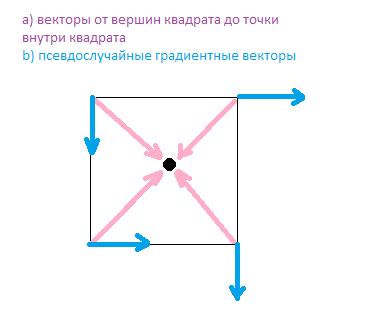
Рассмотрим пару примеров:
Одномерный случай:
Тут все довольно просто. Посмотрите на картинку и попробуйте дать ответ, какое значение (число) получается в точке 7.3:
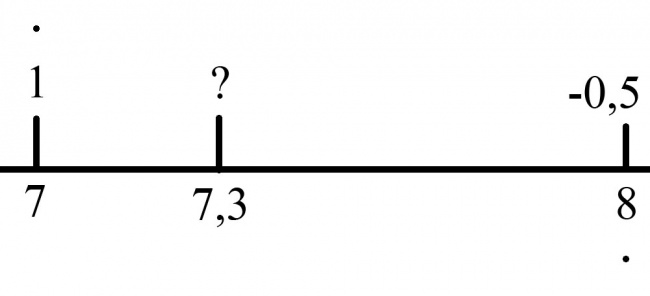
Ответ: 1*0.7 + (-0.5)*0.3 = 0.55
где: 0.7 - локальная координата (8-7.3) для 1 и 0.3 (1-(8-7.3)) для -0.5
Двумерный случай:
Пусть имеется квадрат с векторами исходящими из его углов.
Для расчета нам потребуется все те же локальные координаты и скалярное произведение этих векторов. Если мы поступим таким же образом, как и в одномерном случае, но будем использовать вектора в узлах, вместо простых чисел, то в результате мы получим точку. Чем ближе эта точка к центру квадрата - тем больше значение в этой точке.
Когда мы получим по одному значению в каждом квадрате интерполируем функцию. Таким образом в зависимости от ближайших значений квадратов мы получим пересекающиеся полусферы разного радиуса. Когда мы сопоставим эти значения с числами (например, высота функции), то можно из этих значений построить картинку как в начале статьи.
Сглаживание значений:
Значения конечно же можно сгладить линейно, но разве это будет красиво? Можно использовать любую функцию, исторически сложилось четыре варианта сглаживания (это я так интерполяцию называю):
1) Билинейная интерполяция самая простая, но и результат не самый привлекательный.
2) Кубическая (-2*t*t*t+3*t*t), но искривление не слишком большое.
3) Косинусное ((1-cos(t*П))/2)
4) И самый привлекательный - уравнение пятой степени (quintic) (t*t*t*(t*(t*6-15)+10))
Другие варианты интерполяции подразумевают модифицирование локальной координаты (параметра t) перед интерполяцией. Получаются более плавные переходы возле граничных значений (0 и 1).




