Уроки, алгоритмы, программы, примеры
Вход на сайт
Новые комментарии
Удаление невидимых граней выпуклого многогранника на JavaScript
Скажите пожалуйста, подскажите алгоритм по которому по заданным точкам можно определить тип многогранника, скажем это куб или прямоугольный параллелепипед. Нашел теорию по этим фигурам:
https://www.mat...
https://www.mat...
Акцентировать внимание...
Подключение OpenGL к Code::Blocks с MinGW
Всем у кого не работает.
файл wizard.script
Ещё одно упоминание Glut32 в строке
"if (!VerifyLibFile(dir_nomacro_lib, _T("glut32"), _T("GLUT's"))) return false;"
меняем на
"if (!VerifyLibFile(dir_nomacro_lib, _T("freeglut"), _T("GLUT's"))) return...
Круговой фрактал C#
Не получается, емаё
Работа с 3-х мерными объектами в Python с использованием OpenGL
огромное спасибо за подробное объяснение про 3д графику на питоне, в интернете очень мало подобной информации
Треугольник Серпинского на SFML
dobryj den, popytalas otkryt prikreplionnyj fail ctoby posmotret kak rabotaet, no mne ego ne pokazyvaet vydajet osibku. Pochemu?
Счетчики и рейтинг
Атрактор Питера де Йонга представлен на странице https://cgraph.ru/node/151
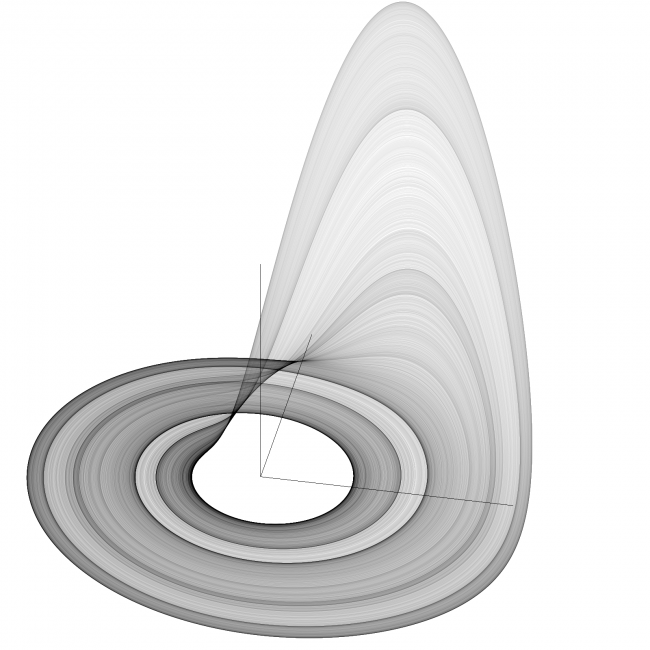
Аттрактор Рёсслера — хаотический аттрактор, которым обладает система дифференциальных уравнений Рёсслера:
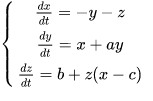
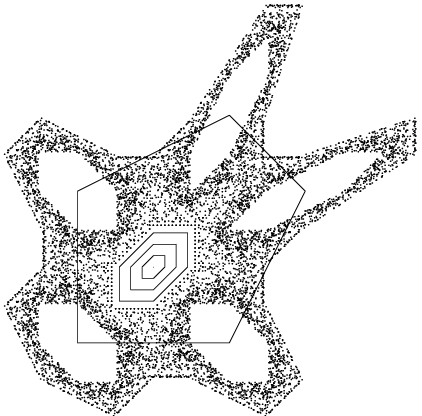
Шум Перлина
Perlin noise (Шум Перлина, также иногда Классический шум Перлина) — математический алгоритм по генерированию процедурной текстуры псевдо-случайным методом. Используется в компьютерной графике для увеличения реализма или графической сложности поверхности геометрических объектов.
Термин «фрактал» (от лат. fractare – ломать, дробить; fractus – расчлененный, разбитый; англ. fractal – дробный) ввел Бенуа Мандельброт (Benoit Mandelbrot), родившийся в Варшаве в 1924 г., работавший во Франции и США.
Бро́уновское де́рево является формой компьютерного искусства, которое было популярно в 1990-х, когда домашние компьютеры стали обладать достаточной производительностью для моделирования броуновского движения (отсюда и название). Броуновские деревья — математические модели древовидных структур, связанных с физическим процессом, известным как агрегация, ограниченная диффузией.
Фрактал Висекка, также известный как снежинка Виссека – фрактал, возникающий из конструкции, подобной конструкции ковра Серпинского, предложенной Томасом Висекком, является одним из двух коробочных фракталов. Он имеет приложения, в том числе пересекающиеся с компактными антеннами, особенно в сотовых телефонах. На данном рисунке изображен фрактал на пятой итерации.
Кривая Госпера, известная также как кривая Пеано-Госпера, названная именем Била Госпера, — это заполняющая пространство кривая. Кривая является фрактальной кривой, подобной кривым дракона и Гильберта. На рисунке приведена четвёртая стадия кривой Госпера.
Круговой фрактал — класс геометрических (конструктивных) фракталов, построенных многократным вписыванием в окружность других окружностей меньшего радиуса.