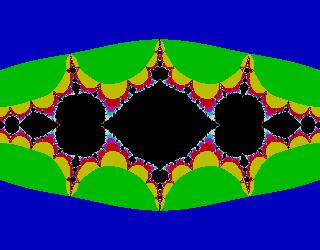
Множества Мандельброта и Жулиа, вероятно, два наиболее распространенных среди сложных фракталов. Их можно найти во многих научных журналах, обложках книг, открытках, и в компьютерных хранителях экрана. Множество Мандельброта, которое было построено Бенуа Мандельбротом, наверное первая ассоциация, возникающая у людей, когда они слышат слово фрактал. Это фрактал, напоминающий чесальную машину с прикрепленными к ней пылающими древовидными и круглыми областями.

Рассмотрим функцию fc:C→C, c∈C. Множество Мандельброта M(f) определяется как множество всех c∈C , для которых орбита точки z=0 при отображении fc(z) ограничена. Наиболее часто используется fc(z)=z2+c. Раскладывая на действительную и мнимую часть, получаем:
Re: x2-y2+a
Im: 2xy+b
приняв, что z=x+yi и c=a+bi. Цвет обычно выбирают по числу итераций, но есть и другие способы.


Также можно изменить вид фрактала, если контроль значения z вести другим образом. Наиболее употребляемый способ уже рассмотрен — z достигает определённого максимального числа. Другими способами являются:
- действительная часть z меньше определённого числа;
- мнимая часть z меньше определённого числа;
- и мнимая, и действительная части z меньше какого-либо числа.
Есть и другие способы.
Ниже приведены изображения для fc(z)=zn+c
z2+c
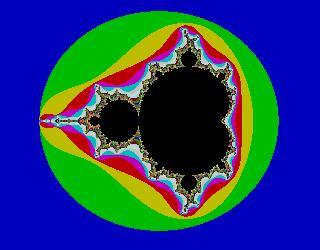
z3+c

z4+c
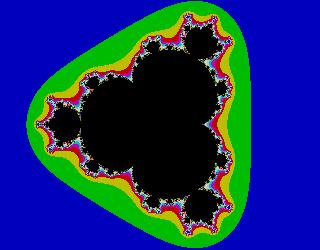
z5+c

Множество Жулиа

Удивительно, но множества Жулиа образуются по той же самой формуле, что и множество Мандельброта. Множество Жулиа было изобретено французским математиком Гастоном Жулиа, по имени которого и было названо множество. Первый вопрос, возникающий после визуального знакомства с множествами Мандельброта и Жулиа это "если оба фрактала сгенерированы по одной формуле, почему они такие разные?" Сначала посмотрите на картинки множества Жулиа. Достаточно странно, но существуют разные типы множеств Жулиа. При рисовании фрактала с использованием различных начальных точек (чтобы начать процесс итераций), генерируются различные изображения. Это применимо только ко множеству Жулиа.
Хотя это нельзя увидеть на картинке, фрактал Мандельброта - это, на самом деле, множество фракталов Жулиа, соединенных вместе. Каждая точка (или координата) множества Мандельброта соответствует фракталу Жулиа.
Рассмотрим функцию f:C→C. ество Жюлиа определяется как граница множества точек z, стремящихся к бесконечности при итерировании f(z):
J(f)= ∂ { z: f(n)(z) → ∞, n → ∞ }
При c=i множество Жюлиа превращается в дендрит:

Другие формулы:
z3+c
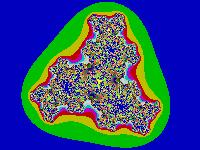
z4+c

ch(z)
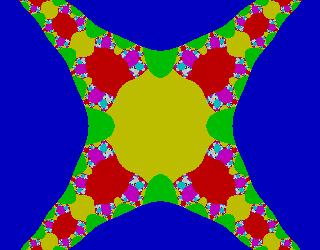
ctg(z)

sin(z)cos(z)
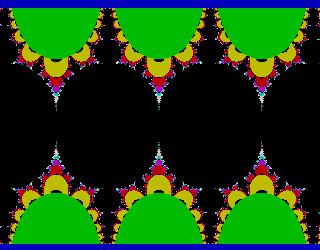
sh(z)
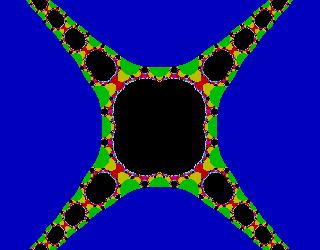
tg(z)

zcos(z)
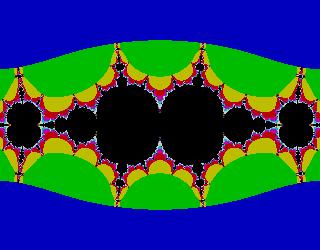
zsin(z)